Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Primzahl: Unterschied zwischen den Versionen
| (8 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== Primzahlen == | == Primzahlen == | ||
Einige Zahlen können gar nicht geteilt werden. Diese Zahlen nennt man '''Primzahlen'''. Primzahlen sind natürliche Zahlen, die nur durch 1 und durch sich selbst teilbar sind. Bei der 1 handelt es sich um keine Primzahl! | Einige Zahlen können gar nicht geteilt werden. Diese Zahlen nennt man '''Primzahlen'''. Primzahlen sind natürliche Zahlen, die nur durch 1 und durch sich selbst teilbar sind. Bei der 1 handelt es sich um keine Primzahl! Dies wurde mathematisch festgelegt. Bereits am Anfang des Zahlsystems begegnet man einer Primzahl, der 2. Die Zahl 2 ist die einzige gerade Primzahl, die nur durch 1 und durch sich selbst (der 2) teilbar ist. Alle anderen Primzahlen sind ungerade Zahlen wie z.B. 7, 41 oder 59 <br /> | ||
2 : 2 = 1 <br /> | 2 : 2 = 1 <br /> | ||
2 : 1 = 2 <br /> | 2 : 1 = 2 <br /> | ||
Eine weitere Zahl, die uns relativ früh im Zahlsystem begegnet, die eine Primzahl ist, ist die 7. | |||
Eine weitere Zahl, die uns relativ früh im Zahlsystem begegnet, die eine Primzahl ist, ist die 7. Die 7 ist nur durch 1 und durch sich selbst (die 7) teilbar, damit es keinen Rest ergibt.<br /> | |||
7 : 7 = 1 <br /> | 7 : 7 = 1 <br /> | ||
7 : 1 = 7 <br /> | 7 : 1 = 7 <br /> | ||
Eine Hilfe, um zu ermitteln, ob es sich um eine Primzahl handelt oder die beliebige Zahl doch einen Teiler hat, sind die '''Teilbarkeitsregeln'''. Bei der anderen Hilfe handelt es sich um das '''Sieb des Eratosthenes'''. Hier | Eine Hilfe, um zu ermitteln, ob es sich um eine Primzahl handelt oder die beliebige Zahl doch einen Teiler hat, sind die '''Teilbarkeitsregeln'''. Bei der anderen Hilfe handelt es sich um das '''Sieb des Eratosthenes'''. Hier die Erläuterung für das Sieb bis zur Zahl 100. | ||
Die 1 streicht man weg, da die 1 keine Primzahl ist. Die 2 wird nicht weggestrichen und ist damit eine Primzahl. Als nächstes müssen alle Zahlen weggestrichen werden, die durch 2 teilbar sind. Damit sind sie keine Primzahlen. Die Zahl 3 darf ebenfalls nicht durchgestrichen werden, weil es eine Primzahl ist. Nun müssen alle Zahlen durchgestrichen werden, die durch 3 teilbar sind. Dieses Prinzip muss jetzt bis zur Zahl 10 weitergeführt werden. Danach weiß man welche Zahlen bis 100 Primzahlen sind und welche nicht. <br /> | |||
Die größte ermittelte Primzahl, die herausgefunden wurde, hat über 22 Millionen Stellen. | |||
[[Datei: | [[Datei:Sieb des Eratosthenes 3.pdf|left|thumb|Sieb des Eratosthenes]] | ||
Aktuelle Version vom 24. Februar 2017, 22:58 Uhr
Primzahlen
Einige Zahlen können gar nicht geteilt werden. Diese Zahlen nennt man Primzahlen. Primzahlen sind natürliche Zahlen, die nur durch 1 und durch sich selbst teilbar sind. Bei der 1 handelt es sich um keine Primzahl! Dies wurde mathematisch festgelegt. Bereits am Anfang des Zahlsystems begegnet man einer Primzahl, der 2. Die Zahl 2 ist die einzige gerade Primzahl, die nur durch 1 und durch sich selbst (der 2) teilbar ist. Alle anderen Primzahlen sind ungerade Zahlen wie z.B. 7, 41 oder 59
2 : 2 = 1
2 : 1 = 2
Eine weitere Zahl, die uns relativ früh im Zahlsystem begegnet, die eine Primzahl ist, ist die 7. Die 7 ist nur durch 1 und durch sich selbst (die 7) teilbar, damit es keinen Rest ergibt.
7 : 7 = 1
7 : 1 = 7
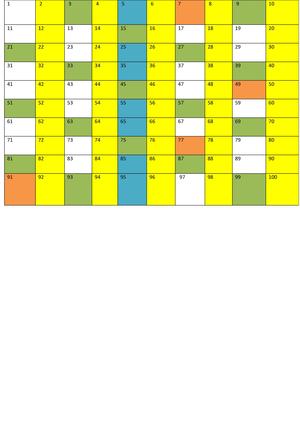
Eine Hilfe, um zu ermitteln, ob es sich um eine Primzahl handelt oder die beliebige Zahl doch einen Teiler hat, sind die Teilbarkeitsregeln. Bei der anderen Hilfe handelt es sich um das Sieb des Eratosthenes. Hier die Erläuterung für das Sieb bis zur Zahl 100.
Die 1 streicht man weg, da die 1 keine Primzahl ist. Die 2 wird nicht weggestrichen und ist damit eine Primzahl. Als nächstes müssen alle Zahlen weggestrichen werden, die durch 2 teilbar sind. Damit sind sie keine Primzahlen. Die Zahl 3 darf ebenfalls nicht durchgestrichen werden, weil es eine Primzahl ist. Nun müssen alle Zahlen durchgestrichen werden, die durch 3 teilbar sind. Dieses Prinzip muss jetzt bis zur Zahl 10 weitergeführt werden. Danach weiß man welche Zahlen bis 100 Primzahlen sind und welche nicht.
Die größte ermittelte Primzahl, die herausgefunden wurde, hat über 22 Millionen Stellen.