Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Runden: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
== Runden auf bestimmte [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Dezimalsystem|Stellenwerte]] == | == Runden auf bestimmte [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Dezimalsystem|Stellenwerte]] == | ||
Wenn man rundet, muss man festlegen auf welche | Wenn man rundet, muss man festlegen auf welche Stelle man runden möchte. | ||
=== Runden auf die Zehnerstelle === | === Runden auf die Zehnerstelle === | ||
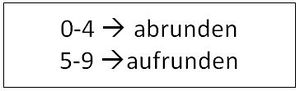
Wenn man auf die Zehnerstelle runden möchte, muss man schauen an welchem Nachbarzehner die Zahl näher dran ist. | Wenn man auf die Zehnerstelle runden möchte, muss man schauen an welchem Nachbarzehner die Zahl näher dran ist. Dazu schaut man sich also die Einerstelle an. Bei 0-4 muss man abrunden und bei 5-9 muss man aufrunden. | ||
<br /> | <br /> | ||
Zum Beispiel ist die Zahl 49 näher an dem Nachbarzehner 50 als an dem Nachbarzehner 40. Deswegen ist 49 rund 50. Man schreibt auch: 49 ~ 50. | Zum Beispiel ist die Zahl 49 näher an dem Nachbarzehner 50 als an dem Nachbarzehner 40. Deswegen ist 49 rund 50. Man schreibt auch: 49 ~ 50. | ||
| Zeile 26: | Zeile 26: | ||
<br /> | <br /> | ||
'''Beispiele'''<br /> | |||
- 74 ist gerundet 70 | - 74 ist gerundet 70 | ||
<br /> | <br /> | ||
| Zeile 35: | Zeile 36: | ||
Beim Runden auf die Hunderterstelle betrachtet man die Zehnerstelle. Man schaut also, an welchem Nachbarhunderter die Zahl näher dran ist. | Beim Runden auf die Hunderterstelle betrachtet man die Zehnerstelle. Man schaut also, an welchem Nachbarhunderter die Zahl näher dran ist. | ||
'''Beispiele''' | |||
- 249 ist gerundet 200 | - 249 ist gerundet 200 | ||
<br /> | <br /> | ||
- 451 ist gerundet 500 | - 451 ist gerundet 500 | ||
[[Datei:Zahlenstrahl 200-300.JPG|thumb|600px|left]] | |||
<br /> | |||
<br /> | |||
<br /> | |||
<br /> | |||
<br /> | |||
=== Runden auf die Tausenderstelle === | === Runden auf die Tausenderstelle === | ||
| Zeile 45: | Zeile 54: | ||
Wenn man auf die Tausenderstelle runden möchte, betrachtet man die Hunderterstelle. Also muss man schauen, an welchem Nachbartausender die Zahl näher dran ist. | Wenn man auf die Tausenderstelle runden möchte, betrachtet man die Hunderterstelle. Also muss man schauen, an welchem Nachbartausender die Zahl näher dran ist. | ||
'''Beispiele''' | |||
- 1499 ist gerundet 1000 | - 1499 ist gerundet 1000 | ||
<br /> | <br /> | ||
- 3695 ist gerundet 4000 | - 3695 ist gerundet 4000 | ||
[[Datei:Zahlenstrahl 3000-4000.JPG|thumb|600px|left]] | |||
<br /> | |||
<br /> | |||
<br /> | |||
<br /> | |||
<br /> | |||
<br /> | |||
== Runden von Dezimalzahlen == | == Runden von Dezimalzahlen == | ||
Wenn eine Zahl viele Kommastellen hat, hilft es diese Zahl zu runden. Das Runden von Dezimalzahlen funktioniert genauso wie das Runden von natürlichen Zahlen. | Wenn eine Zahl viele Kommastellen hat, hilft es diese Zahl zu runden. Das Runden von Dezimalzahlen funktioniert genauso wie das Runden von natürlichen Zahlen. | ||
'''Beispiele'''<br /> | |||
Um die Zahl 1,4538 auf die erste Stelle nach dem Komma zu runden, betrachtet man die zweite Stelle nach dem Komma. Da dort die Zahl 5 steht, rundet man auf und die Zahl 1,4538 ist rund 1,5. Wenn man keine Kommazahl möchte, muss man die erste Zahl nach dem Komma betrachten. Weil dort die 4 steht, muss man abrunden. Deswegen ist die Zahl 1,4538 gerundet 1. | Um die Zahl 1,4538 auf die erste Stelle nach dem Komma zu runden, betrachtet man die zweite Stelle nach dem Komma. Da dort die Zahl 5 steht, rundet man auf und die Zahl 1,4538 ist rund 1,5. Wenn man keine Kommazahl möchte, muss man die erste Zahl nach dem Komma betrachten. Weil dort die 4 steht, muss man abrunden. Deswegen ist die Zahl 1,4538 gerundet 1. | ||
== Spezialfall == | == Spezialfall == | ||
Als Spezialfälle | Als Spezialfälle kann man Zahlen bezeichnen, die bereits gerundet aussehen, wie die Zahl 2100. Bei dieser Zahl ist es auf den ersten Blick schwer, auf die Hunderterstelle zu runden. Und dabei ist das so einfach. Denn die Zahl 2100 ist gerundet auch die Zahl 2100. Hier schreibt man aber 2100 = 2100. | ||
== Rechnen mit gerundeten Zahlen == | == Rechnen mit gerundeten Zahlen == | ||
Oft rechnet man mit gerundeten Zahlen, weil das leichter fällt. Dieses Rechnen nennt man [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Überschlag|Überschlag]]. | Oft rechnet man mit gerundeten Zahlen, weil das leichter fällt. Dieses Rechnen nennt man [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Überschlag|Überschlag]]. Außerdem kann man durch die Überschlagsrechnung schauen, ob das Ergebnis im richtigen Bereich liegt. Soll man zum Beispiel ausrechnen was das Ergebnis von 356+28 ist, so rechnet man im Überschlag 360+30=390. Damit weiß man, dass das Ergebnis von 356+28 ungefähr im Bereich von 390 liegen muss. | ||
Aktuelle Version vom 27. Februar 2017, 16:53 Uhr
Definition
Man rundet, um sich eine Zahl leichter merken oder damit rechnen zu können. Wenn man rundet, möchte man eine Zahl vereinfachen.
Allgemeine Rundungsregel
Bei den Zahlen 0,1,2,3 und 4 wird abgerundet.
Bei den Zahlen 5,6,7,8 und 9 wird aufgerundet.
Runden auf bestimmte Stellenwerte
Wenn man rundet, muss man festlegen auf welche Stelle man runden möchte.
Runden auf die Zehnerstelle
Wenn man auf die Zehnerstelle runden möchte, muss man schauen an welchem Nachbarzehner die Zahl näher dran ist. Dazu schaut man sich also die Einerstelle an. Bei 0-4 muss man abrunden und bei 5-9 muss man aufrunden.
Zum Beispiel ist die Zahl 49 näher an dem Nachbarzehner 50 als an dem Nachbarzehner 40. Deswegen ist 49 rund 50. Man schreibt auch: 49 ~ 50.
Beispiele
- 74 ist gerundet 70
- 78 ist gerundet 80
Runden auf die Hunderterstelle
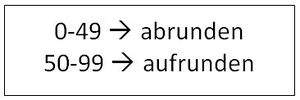
Beim Runden auf die Hunderterstelle betrachtet man die Zehnerstelle. Man schaut also, an welchem Nachbarhunderter die Zahl näher dran ist.
Beispiele
- 249 ist gerundet 200
- 451 ist gerundet 500
Runden auf die Tausenderstelle
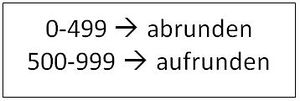
Wenn man auf die Tausenderstelle runden möchte, betrachtet man die Hunderterstelle. Also muss man schauen, an welchem Nachbartausender die Zahl näher dran ist.
Beispiele
- 1499 ist gerundet 1000
- 3695 ist gerundet 4000
Runden von Dezimalzahlen
Wenn eine Zahl viele Kommastellen hat, hilft es diese Zahl zu runden. Das Runden von Dezimalzahlen funktioniert genauso wie das Runden von natürlichen Zahlen.
Beispiele
Um die Zahl 1,4538 auf die erste Stelle nach dem Komma zu runden, betrachtet man die zweite Stelle nach dem Komma. Da dort die Zahl 5 steht, rundet man auf und die Zahl 1,4538 ist rund 1,5. Wenn man keine Kommazahl möchte, muss man die erste Zahl nach dem Komma betrachten. Weil dort die 4 steht, muss man abrunden. Deswegen ist die Zahl 1,4538 gerundet 1.
Spezialfall
Als Spezialfälle kann man Zahlen bezeichnen, die bereits gerundet aussehen, wie die Zahl 2100. Bei dieser Zahl ist es auf den ersten Blick schwer, auf die Hunderterstelle zu runden. Und dabei ist das so einfach. Denn die Zahl 2100 ist gerundet auch die Zahl 2100. Hier schreibt man aber 2100 = 2100.
Rechnen mit gerundeten Zahlen
Oft rechnet man mit gerundeten Zahlen, weil das leichter fällt. Dieses Rechnen nennt man Überschlag. Außerdem kann man durch die Überschlagsrechnung schauen, ob das Ergebnis im richtigen Bereich liegt. Soll man zum Beispiel ausrechnen was das Ergebnis von 356+28 ist, so rechnet man im Überschlag 360+30=390. Damit weiß man, dass das Ergebnis von 356+28 ungefähr im Bereich von 390 liegen muss.