Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Länge: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (11 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Eine Länge gibt in der Mathematik die Entfernung zwischen zwei Punkten an. Es wird der direkte Weg zwischen beiden Punkten ermittelt. Dies nennt man auch die Strecke zwischen zwei Punkten. | |||
=== Bestimmen der Länge === | === Bestimmen der Länge === | ||
Im Alltag bestimmt man die Länge meistens durch Messen. In der Mathematik besteht aber auch die Möglichkeit, Längen zu berechnen. | |||
Zum Messen einer Länge gibt es verschiedene Werkzeuge: Lineal, Geodreieck, Zollstock, Maßband und noch viele mehr. | Zum Messen einer Länge gibt es verschiedene Werkzeuge: Lineal, Geodreieck, Zollstock, Maßband und noch viele mehr. | ||
Will man zum Beispiel die Länge eines Stiftes bestimmen, | Will man zum Beispiel die Länge eines Stiftes bestimmen, eignet sich ein Lineal. Man legt die Minenspitze genau bei der Null des Lineals an und liest am Ende des Stiftes die Länge ab <ref>Messen mit einem Lineal: http://www.kinderfunkkolleg-mathematik.de/lucy-fragt/messen</ref>. | ||
[[Datei:Längenmessung Stift.jpg|thumb|rechts|Messung der Länge eines Stiftes mit einem Lineal]] | [[Datei:Längenmessung Stift.jpg|thumb|rechts|Messung der Länge eines Stiftes mit einem Lineal]] | ||
| Zeile 19: | Zeile 19: | ||
Datei:Massband.jpg|Maßband | Datei:Massband.jpg|Maßband | ||
</gallery> | </gallery> | ||
=== Längeneinheit === | === Längeneinheit === | ||
| Zeile 32: | Zeile 33: | ||
|- | |- | ||
| Zentimeter || cm | | Zentimeter || cm | ||
|- | |||
| Dezimeter || dm | |||
|- | |- | ||
| Meter || m | | Meter || m | ||
|- | |- | ||
| Kilometer || km | | Kilometer || km | ||
|} | |||
In Amerika werden Längen hingegen in inch (Zoll), foot (Fuß), yard (Schritt) und mile (Meile) angegeben. Dies nennt man das angloamerikanische Maßsystem. | |||
=== Umwandlung von Einheiten === | |||
Im metrischen System kann man jede Längeneinheit in eine andere Längeneinheit umwandeln. Dies benötigt man zum Beispiel, wenn man mit Längen rechnen will. Folgende Aufzählung zeigt, wie man die einzelnen Einheiten umrechnet: | |||
{| | |||
|- | |||
| '''1 mm''' || = || 0,1 cm || = || 0,01 dm || = || 0,001 m || = || 0,000001 km | |||
|- | |||
| '''1 cm''' || = || 10 mm || = || 0,1 dm || = || 0,01 m || = || 0,00001 km | |||
|- | |||
| '''1 dm''' || = || 100 mm || = || 10 cm || = || 0,1 m || = || 0,0001 km | |||
|- | |||
| '''1 m''' || = || 1000 mm || = || 100 cm || = || 10 dm || = || 0,001 km | |||
|- | |||
| '''1 km''' || = || 1 000 000 mm || = || 100 000 cm || = || 10 000 dm || = || 1000 m | |||
|} | |} | ||
=== Beispiele für Längen === | === Beispiele für Längen === | ||
Um sich Längen gut vorstellen zu können, ist es hilfreich, sich bestimmte Gegenstände und ihre Längen einzuprägen. Dies nennt man Stützpunktvorstellungen. Diese können helfen, sich Längen im Alltag vorzustellen. | Um sich Längen gut vorstellen zu können, ist es hilfreich, sich bestimmte Gegenstände und ihre Längen einzuprägen. Dies nennt man Stützpunktvorstellungen. Diese können helfen, sich bestimmte Längen im Alltag besser vorzustellen. In der folgenden Tabelle sind einige Beispiele genannt. Natürlich kann man auch ganz andere Gegenstände und deren Länge als Stützpunktvorstellung nutzen. | ||
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 49: | Zeile 71: | ||
| Durchmesser einer 10 Cent-Münze || 2cm | | Durchmesser einer 10 Cent-Münze || 2cm | ||
|- | |- | ||
| Länge | | Länge einer Streichholzschachtel || 5cm | ||
|- | |||
| Höhe einer Toilettenpapierrolle || 10cm | |||
|- | |- | ||
| äußerer, klappbarer Teil einer Schultafel || 1m | | äußerer, klappbarer Teil einer Schultafel || 1m | ||
| Zeile 57: | Zeile 81: | ||
| ovale Laufbahn in einem Stadion|| 400m | | ovale Laufbahn in einem Stadion|| 400m | ||
|} | |} | ||
=== Rechnen mit Längen === | === Rechnen mit Längen === | ||
Mit Längen kann man auch rechnen. Dies geht jedoch nur, wenn diese Längen die gleiche Einheit besitzen. Ist dies nicht der Fall, dann kann man diese Einheiten umwandeln, sodass sie gleich sind. | Mit Längen kann man auch rechnen. Dies geht jedoch nur, wenn diese Längen die gleiche Einheit besitzen. Ist dies nicht der Fall, dann kann man diese Einheiten umwandeln, sodass sie gleich sind. Längen kann man addieren, subtrahieren, multiplizieren, vergleichen und der Größe nach ordnen. | ||
[[Datei:Addition Länge.JPG|thumb|links|Beispiel der Addition von Längen]] | [[Datei:Addition Länge.JPG|thumb|links|Beispiel der Addition von Längen]] | ||
| Zeile 70: | Zeile 94: | ||
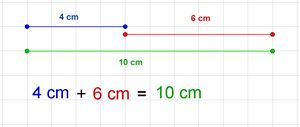
In dieser Beispielrechnung werden zwei Längen miteinander addiert. Dies geschieht, indem die rote Strecke (6cm) an die blaue Strecke (4cm) angelegt wird. Hierdurch entsteht eine Strecke, die 10cm lang ist (grüne Strecke). Dies ist das Ergebnis der Addition. Bei einer Addition zweier Strecken werden also die Strecken hintereinandergelegt und zusammen gemessen. | |||
==Einzelnachweise== | ==Einzelnachweise== | ||
<references> | <references> | ||
Aktuelle Version vom 3. Februar 2017, 10:48 Uhr
Eine Länge gibt in der Mathematik die Entfernung zwischen zwei Punkten an. Es wird der direkte Weg zwischen beiden Punkten ermittelt. Dies nennt man auch die Strecke zwischen zwei Punkten.
Bestimmen der Länge
Im Alltag bestimmt man die Länge meistens durch Messen. In der Mathematik besteht aber auch die Möglichkeit, Längen zu berechnen.
Zum Messen einer Länge gibt es verschiedene Werkzeuge: Lineal, Geodreieck, Zollstock, Maßband und noch viele mehr.
Will man zum Beispiel die Länge eines Stiftes bestimmen, eignet sich ein Lineal. Man legt die Minenspitze genau bei der Null des Lineals an und liest am Ende des Stiftes die Länge ab [1].
Zum Messen der Länge eines Tisches nutzt man besser einen Zollstock. Für größere Längen braucht man ein Maßband oder spezielle Messwerkzeuge. Sehr kurze Längen misst man beispielsweise mit einem Messschieber.
Längeneinheit
Es gibt viele verschiedene Möglichkeiten die Länge anzugeben. In Deutschland ist es üblich das metrische System[2] zu verwenden.
Typische Längeneinheiten sind:
| Einheit | Symbol |
|---|---|
| Millimeter | mm |
| Zentimeter | cm |
| Dezimeter | dm |
| Meter | m |
| Kilometer | km |
In Amerika werden Längen hingegen in inch (Zoll), foot (Fuß), yard (Schritt) und mile (Meile) angegeben. Dies nennt man das angloamerikanische Maßsystem.
Umwandlung von Einheiten
Im metrischen System kann man jede Längeneinheit in eine andere Längeneinheit umwandeln. Dies benötigt man zum Beispiel, wenn man mit Längen rechnen will. Folgende Aufzählung zeigt, wie man die einzelnen Einheiten umrechnet:
| 1 mm | = | 0,1 cm | = | 0,01 dm | = | 0,001 m | = | 0,000001 km |
| 1 cm | = | 10 mm | = | 0,1 dm | = | 0,01 m | = | 0,00001 km |
| 1 dm | = | 100 mm | = | 10 cm | = | 0,1 m | = | 0,0001 km |
| 1 m | = | 1000 mm | = | 100 cm | = | 10 dm | = | 0,001 km |
| 1 km | = | 1 000 000 mm | = | 100 000 cm | = | 10 000 dm | = | 1000 m |
Beispiele für Längen
Um sich Längen gut vorstellen zu können, ist es hilfreich, sich bestimmte Gegenstände und ihre Längen einzuprägen. Dies nennt man Stützpunktvorstellungen. Diese können helfen, sich bestimmte Längen im Alltag besser vorzustellen. In der folgenden Tabelle sind einige Beispiele genannt. Natürlich kann man auch ganz andere Gegenstände und deren Länge als Stützpunktvorstellung nutzen.
| Stützpunktvorstellung | zugehörige Länge |
|---|---|
| Breite eines Fingernagels | ~ 1cm |
| Durchmesser einer 10 Cent-Münze | 2cm |
| Länge einer Streichholzschachtel | 5cm |
| Höhe einer Toilettenpapierrolle | 10cm |
| äußerer, klappbarer Teil einer Schultafel | 1m |
| Höhe einer Zimmertür | 2m |
| ovale Laufbahn in einem Stadion | 400m |
Rechnen mit Längen
Mit Längen kann man auch rechnen. Dies geht jedoch nur, wenn diese Längen die gleiche Einheit besitzen. Ist dies nicht der Fall, dann kann man diese Einheiten umwandeln, sodass sie gleich sind. Längen kann man addieren, subtrahieren, multiplizieren, vergleichen und der Größe nach ordnen.
In dieser Beispielrechnung werden zwei Längen miteinander addiert. Dies geschieht, indem die rote Strecke (6cm) an die blaue Strecke (4cm) angelegt wird. Hierdurch entsteht eine Strecke, die 10cm lang ist (grüne Strecke). Dies ist das Ergebnis der Addition. Bei einer Addition zweier Strecken werden also die Strecken hintereinandergelegt und zusammen gemessen.
Einzelnachweise
<references>
- ↑ Messen mit einem Lineal: http://www.kinderfunkkolleg-mathematik.de/lucy-fragt/messen
- ↑ Kinderfunkkolleg zur Entstehung des metrischen Systems: http://www.kinderfunkkolleg-mathematik.de/themen/wie-kam-es-zum-urmeter