Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Dezimalsystem: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (8 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== Definition == | == Definition == | ||
Das Dezimalsystem ist ein Stellenwertsystem. [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Zahlsystem|Zahlensysteme]], die zu den Stellenwertsystemen gehören, haben immer eine Basis. | Das Dezimalsystem ist ein Stellenwertsystem. [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Zahlsystem|Zahlensysteme]], die zu den Stellenwertsystemen gehören, haben immer eine Basis. Das Dezimalsystem hat die Basis 10. Deshalb kann man es als Zehnersystem bezeichnen. Hierdurch lässt sich gleichzeitig der Name erklären, denn „dezi“ steht für „Zehn“. Man verwendet die zehn arabischen Ziffern 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Ab der Zahl 10 setzt man die Zahlen aus mehreren Ziffern zusammen. In einer Stellenwerttafel würde man die 9 noch in die Spalte der Einer schreiben. Die 10 jedoch nicht mehr, da zehn Einer einen Zehner bilden. Es werden zwei Ziffern benötigt. Man schreibt eine 0 in die Einerspalte und eine 1 in die Zehnerspalte. Dies kann auch als Stellenwertüberschreitung bezeichnet werden. | ||
== Bündelung == | == Bündelung == | ||
Das Dezimalsystem lässt sich mit Hilfe der fortgesetzten Bündelung erklären. Bündelung bedeutet, dass immer eine bestimmte Anzahl an Einheiten zusammengefasst wird. Eine Bündelung führt zum nächsten Stellenwert, sobald ein Bündel voll besetzt ist. | Das Dezimalsystem lässt sich mit Hilfe der fortgesetzten Bündelung erklären. Bündelung bedeutet, dass immer eine bestimmte Anzahl an Einheiten zusammengefasst wird. Im Dezimalsystem werden immer zehn Einheiten gebündelt. Eine Bündelung führt zum nächsten Stellenwert, sobald ein Bündel voll besetzt ist. Dies wird von Stellenwert zu Stellenwert fortgeführt. Man beginnt mit den Einern und setzt die Bündelung in Zehner, Hunderter, Tausender, Zehntausender,... fort. | ||
[[Datei:Bündelung.jpg|thumb|]] | [[Datei:Bündelung.jpg|thumb|]] | ||
==== Beispiel ==== | ==== Beispiel ==== | ||
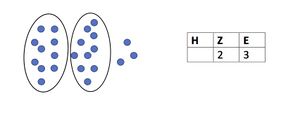
So können beispielsweise 23 Punkte in zwei Zehner und drei Einer gebündelt werden. Aus diesem Grund steht die 2 in der Zehnerspalte und die 3 in der Einerspalte, wenn man die 23 in eine Stellenwerttafel einträgt. | So können beispielsweise 23 Punkte in zwei Zehner und drei Einer gebündelt werden. Aus diesem Grund steht die 2 in der Zehnerspalte und die 3 in der Einerspalte, wenn man die 23 in eine Stellenwerttafel einträgt. | ||
Für eine nicht besetzte Stelle schreibt man eine | Für eine nicht besetzte Stelle schreibt man eine 0. Das bedeutet, dass keine Bündelung für diesen Stellenwert vorhanden ist. Die Einer sind eine Ausnahme, denn an diesem Stellenwert sind keine Bündel zu finden. Es wird nur eine 0 geschrieben, wenn keine Einer vorhanden sind. Ein Beispiel hierfür ist die 408. Wenn man wie bei der Zahl 23 vorgeht, kann die 408 vorerst in 40 Zehner und acht Einer gebündelt werden. Ein Bündel mit zehn Einheiten ist aber voll besetzt. Die 40 Zehner werden erneut zu vier Hunderten gebündelt, denn zehn Zehner ergeben einen Hunderter. In der Stellenwerttafel wird nun die 4 in die Hunderterspalte eingetragen und in der Zehnerspalte steht die 0, da es keine Zehnerbündel gibt. Die 8 wird in die Einerspalte eingetragen. [[Datei:Dienes Material.jpg|thumb|Dienes Material | 160px]] | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Zeile 16: | Zeile 17: | ||
| 4 || 0 || 8 | | 4 || 0 || 8 | ||
|} | |} | ||
Man kann verschiedene Hilfen nutzen, die die Bündelung verdeutlichen. | |||
== Geschichte == | == Geschichte == | ||
Das Dezimalsystem gibt es bereits seit einiger Zeit. In den Jahren 628-629 n. Chr. setzten sich das Stellenwertsystem und das Nullzeichen in Indien durch. Im 13. und 14. Jahrhundert n. Chr. wurde in Westeuropa | Das Dezimalsystem gibt es bereits seit einiger Zeit. In den Jahren 628-629 n. Chr. setzten sich das Stellenwertsystem und das Nullzeichen in Indien durch. Im 13. und 14. Jahrhundert n. Chr. wurde in Westeuropa zum ersten Mal schriftlich mit Ziffern gerechnet. Hieraus hat sich das Dezimalsystem entwickelt. Heute ist es internationaler Standard. Das heißt, dass die meisten Menschen auf der Welt das Dezimalsystem kennen und benutzen. | ||
Aktuelle Version vom 14. Februar 2017, 06:58 Uhr
Definition
Das Dezimalsystem ist ein Stellenwertsystem. Zahlensysteme, die zu den Stellenwertsystemen gehören, haben immer eine Basis. Das Dezimalsystem hat die Basis 10. Deshalb kann man es als Zehnersystem bezeichnen. Hierdurch lässt sich gleichzeitig der Name erklären, denn „dezi“ steht für „Zehn“. Man verwendet die zehn arabischen Ziffern 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Ab der Zahl 10 setzt man die Zahlen aus mehreren Ziffern zusammen. In einer Stellenwerttafel würde man die 9 noch in die Spalte der Einer schreiben. Die 10 jedoch nicht mehr, da zehn Einer einen Zehner bilden. Es werden zwei Ziffern benötigt. Man schreibt eine 0 in die Einerspalte und eine 1 in die Zehnerspalte. Dies kann auch als Stellenwertüberschreitung bezeichnet werden.
Bündelung
Das Dezimalsystem lässt sich mit Hilfe der fortgesetzten Bündelung erklären. Bündelung bedeutet, dass immer eine bestimmte Anzahl an Einheiten zusammengefasst wird. Im Dezimalsystem werden immer zehn Einheiten gebündelt. Eine Bündelung führt zum nächsten Stellenwert, sobald ein Bündel voll besetzt ist. Dies wird von Stellenwert zu Stellenwert fortgeführt. Man beginnt mit den Einern und setzt die Bündelung in Zehner, Hunderter, Tausender, Zehntausender,... fort.
Beispiel
So können beispielsweise 23 Punkte in zwei Zehner und drei Einer gebündelt werden. Aus diesem Grund steht die 2 in der Zehnerspalte und die 3 in der Einerspalte, wenn man die 23 in eine Stellenwerttafel einträgt.
Für eine nicht besetzte Stelle schreibt man eine 0. Das bedeutet, dass keine Bündelung für diesen Stellenwert vorhanden ist. Die Einer sind eine Ausnahme, denn an diesem Stellenwert sind keine Bündel zu finden. Es wird nur eine 0 geschrieben, wenn keine Einer vorhanden sind. Ein Beispiel hierfür ist die 408. Wenn man wie bei der Zahl 23 vorgeht, kann die 408 vorerst in 40 Zehner und acht Einer gebündelt werden. Ein Bündel mit zehn Einheiten ist aber voll besetzt. Die 40 Zehner werden erneut zu vier Hunderten gebündelt, denn zehn Zehner ergeben einen Hunderter. In der Stellenwerttafel wird nun die 4 in die Hunderterspalte eingetragen und in der Zehnerspalte steht die 0, da es keine Zehnerbündel gibt. Die 8 wird in die Einerspalte eingetragen.
| H | Z | E |
|---|---|---|
| 4 | 0 | 8 |
Man kann verschiedene Hilfen nutzen, die die Bündelung verdeutlichen.
Geschichte
Das Dezimalsystem gibt es bereits seit einiger Zeit. In den Jahren 628-629 n. Chr. setzten sich das Stellenwertsystem und das Nullzeichen in Indien durch. Im 13. und 14. Jahrhundert n. Chr. wurde in Westeuropa zum ersten Mal schriftlich mit Ziffern gerechnet. Hieraus hat sich das Dezimalsystem entwickelt. Heute ist es internationaler Standard. Das heißt, dass die meisten Menschen auf der Welt das Dezimalsystem kennen und benutzen.