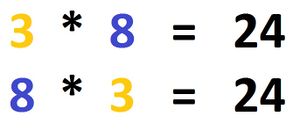Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Tauschaufgabe: Unterschied zwischen den Versionen
Aus ZUM Grundschullernportal
< Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler | Mathelexikon WiSe 16 17
(Die Seite wurde neu angelegt: „== Tauschaufgabe == Bei Tauschaufgaben wird die Reihenfolge der Zahlen, mit denen man rechnet, verändert. <br /> Das kann man bei der Addition und der Multi…“) |
Keine Bearbeitungszusammenfassung |
||
| Zeile 5: | Zeile 5: | ||
Das kann man bei der Addition und der Multiplikation machen. <br /> | Das kann man bei der Addition und der Multiplikation machen. <br /> | ||
== Das Kommutativgesetz == | |||
Die Tauschaufgabe basiert auf dem Kommutativgesetz. Dieses Gesetz besagt, dass beim Addieren und Multiplizieren die Reihenfolge, in der die Zahlen stehen, keinen Unterschied macht. Das Ergebnis bleibt also immer gleich, egal welche der Zahlen vorne steht. Rechnet man 4 + 7 lautet das Ergebnis 11. Tauscht man die beiden Zahlen und rechnet 7 + 4 verändert sich das Ergebnis nicht, es ist noch immer 11. Genau so funktioniert es auch bei der Multiplikation.<br /> | |||
[[Datei:Tauschaufgabe Addition.jpg|thumb|Tauschaufgabe Addition]] | |||
| | |||
[[Datei:Tauschaufgabe Multiplikation.jpg|thumb|Tauschaufgabe Multiplikation]] | |||
| | |||
==Verwendung == | |||
Tauschaufgaben kann man verwenden, um Rechnungen zu vereinfachen. Es ist zum Beispiel leichter, 2 * 17 zu rechnen, als 17 * 2. | |||
Version vom 17. Januar 2017, 15:22 Uhr
Tauschaufgabe
Bei Tauschaufgaben wird die Reihenfolge der Zahlen, mit denen man rechnet, verändert.
Das kann man bei der Addition und der Multiplikation machen.
Das Kommutativgesetz
Die Tauschaufgabe basiert auf dem Kommutativgesetz. Dieses Gesetz besagt, dass beim Addieren und Multiplizieren die Reihenfolge, in der die Zahlen stehen, keinen Unterschied macht. Das Ergebnis bleibt also immer gleich, egal welche der Zahlen vorne steht. Rechnet man 4 + 7 lautet das Ergebnis 11. Tauscht man die beiden Zahlen und rechnet 7 + 4 verändert sich das Ergebnis nicht, es ist noch immer 11. Genau so funktioniert es auch bei der Multiplikation.
Verwendung
Tauschaufgaben kann man verwenden, um Rechnungen zu vereinfachen. Es ist zum Beispiel leichter, 2 * 17 zu rechnen, als 17 * 2.