Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Viereck: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 2: | Zeile 2: | ||
Das '''Viereck''' ist eine geometrische und [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Ebene Figuren|ebene Figur]]. Vierecke gehören zu den Vielecken, das heißt die Figur hat mehrere Ecken. Das Viereck besitzt vier Ecken. Das ist auch der Grund, weshalb es Viereck heißt. | Das '''Viereck''' ist eine geometrische und [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Ebene Figuren|ebene Figur]]. Vierecke gehören zu den Vielecken, das heißt die Figur hat mehrere Ecken. Das Viereck besitzt vier Ecken. Das ist auch der Grund, weshalb es Viereck heißt. | ||
Ein Viereck hat nicht nur vier Ecken, sondern auch vier Seiten. Zwischen zwei Seiten liegt ein [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Winkel|Winkel]]. Dabei können die Seiten unterschiedlich lang und die Winkel unterschiedlich groß sein. Daraus ergeben sich verschiedene Arten von Vierecken. Jedoch haben alle Vierecke eine weitere Gemeinsamkeit. Die Innenwinkelsumme beträgt 360°, das heißt alle Winkel | Ein Viereck hat nicht nur vier Ecken, sondern auch vier Seiten. Zwischen zwei Seiten liegt ein [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Winkel|Winkel]]. Dabei können die Seiten unterschiedlich lang und die Winkel unterschiedlich groß sein. Daraus ergeben sich verschiedene Arten von Vierecken. Jedoch haben alle Vierecke eine weitere Gemeinsamkeit. Die Innenwinkelsumme eines Vierecks beträgt 360°, das heißt alle Winkel innerhalb eines Vierecks ergeben addiert 360°. Bekannte Vierecke sind zum Beispiel das [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Quadrat|Quadrat]], das [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Rechteck|Rechteck]], die [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Raute|Raute]], das Parallelogramm, der [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Drachen|Drachen]] und das Trapez. | ||
[[Datei:Six Quadrilaterals.svg|miniatur|zentriert|Regelmäßige Vierecke]] | [[Datei:Six Quadrilaterals.svg|miniatur|zentriert|Regelmäßige Vierecke]] | ||
Version vom 24. Januar 2017, 18:13 Uhr
Definition
Das Viereck ist eine geometrische und ebene Figur. Vierecke gehören zu den Vielecken, das heißt die Figur hat mehrere Ecken. Das Viereck besitzt vier Ecken. Das ist auch der Grund, weshalb es Viereck heißt.
Ein Viereck hat nicht nur vier Ecken, sondern auch vier Seiten. Zwischen zwei Seiten liegt ein Winkel. Dabei können die Seiten unterschiedlich lang und die Winkel unterschiedlich groß sein. Daraus ergeben sich verschiedene Arten von Vierecken. Jedoch haben alle Vierecke eine weitere Gemeinsamkeit. Die Innenwinkelsumme eines Vierecks beträgt 360°, das heißt alle Winkel innerhalb eines Vierecks ergeben addiert 360°. Bekannte Vierecke sind zum Beispiel das Quadrat, das Rechteck, die Raute, das Parallelogramm, der Drachen und das Trapez.
Vierecke im Alltag
Deshalb bezeichnet man es als eine Fläche.
Haus der Vierecke
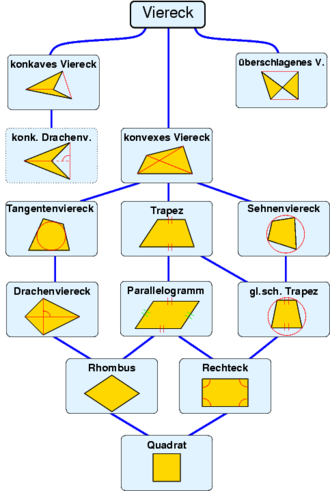
Das Haus der Vierecke zeigt die Beziehungen zwischen den verschiedenen Vierecken. Die Linien zwischen den Vierecken stehen für "ist auch ein...". Zum Beispiel: Jedes Quadrat ist auch ein Rechteck. Jedes Viereck hat verschiedene Eigenschaften. Das Quadrat hat die gleichen Eigenschaften wie ein Rechteck. Allerdings ist es ein Sonderfall des Rechtecks, da beim Rechteck nicht alle Seiten gleich lang sein müssen.