Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Drachen: Unterschied zwischen den Versionen
Aus ZUM Grundschullernportal
< Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler | Mathelexikon WiSe 16 17
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 3: | Zeile 3: | ||
Man kann zwischen dem schiefen Drachen und dem symmetrischen Drachen unterscheiden. | Man kann zwischen dem schiefen Drachen und dem symmetrischen Drachen unterscheiden. | ||
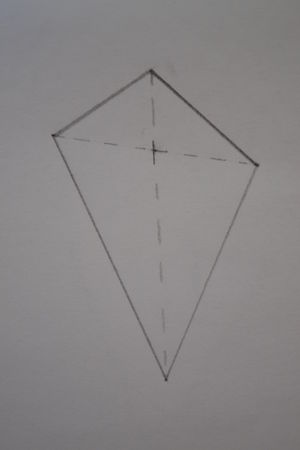
Der schiefe Drachen ist ein Viereck, welches nur die Eigenschaft hat, dass eine Diagonale (Diagonale = die Verbindung von zwei gegenüberliegenden Ecken) von der anderen halbiert wird. | Der '''schiefe Drachen''' ist ein Viereck, welches nur die Eigenschaft hat, dass eine Diagonale (Diagonale = die Verbindung von zwei gegenüberliegenden Ecken) von der anderen halbiert wird. | ||
[[Datei:Schiefer Drachen.JPG|thumb|links|Bild eines schiefen Drachens]] | [[Datei:Schiefer Drachen.JPG|thumb|links|Bild eines schiefen Drachens]] | ||
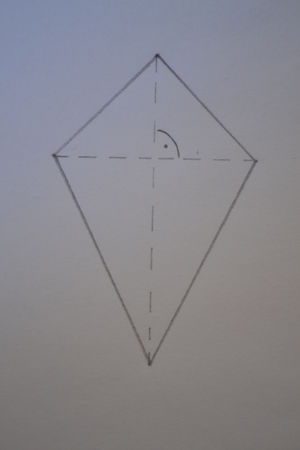
Beim symmetrischen Drachen wird auch eine Diagonale von der anderen halbiert. Außerdem hat er noch folgene Eigenschaften: | Beim '''symmetrischen Drachen''' wird auch eine Diagonale von der anderen halbiert. Außerdem hat er noch folgene Eigenschaften: | ||
* er ist achsensymmetrisch | * er ist achsensymmetrisch | ||
* eine Diagonale wird von der anderen halbiert (wie beim schiefen Drachen) | * eine Diagonale wird von der anderen halbiert (wie beim schiefen Drachen) | ||
Version vom 25. Februar 2017, 13:42 Uhr
Der Drachen ist ein besonderes Viereck.
Man kann zwischen dem schiefen Drachen und dem symmetrischen Drachen unterscheiden.
Der schiefe Drachen ist ein Viereck, welches nur die Eigenschaft hat, dass eine Diagonale (Diagonale = die Verbindung von zwei gegenüberliegenden Ecken) von der anderen halbiert wird.
Beim symmetrischen Drachen wird auch eine Diagonale von der anderen halbiert. Außerdem hat er noch folgene Eigenschaften:
- er ist achsensymmetrisch
- eine Diagonale wird von der anderen halbiert (wie beim schiefen Drachen)
- die Diagonalen stehen senkrecht aufeinander
- es gibt zwei Paar gleich lange benachbarte Seiten
- es gibt ein Paar gleich große gegenüberliegende Winkel
Die Raute ist auch ein symmetrischer Drachen, bei dem alle Seiten gleich lang sind.