Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Umfang: Unterschied zwischen den Versionen
Aus ZUM Grundschullernportal
< Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler | Mathelexikon WiSe 16 17
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
== Der Umfang == | == '''Der Umfang''' == | ||
| Zeile 9: | Zeile 9: | ||
== Umfangsberechnung Ebener Figuren == | === Umfangsberechnung Ebener Figuren === | ||
Um den Umfang eines Vielecks zu berechnen, musst du alle Seiten addieren. | Um den Umfang eines Vielecks zu berechnen, musst du alle Seiten addieren. | ||
=== Umfang Rechteck === | ==== Umfang Rechteck ==== | ||
[[Datei:Umfang Rechteck.png|thumb||330px|left]] | [[Datei:Umfang Rechteck.png|thumb||330px|left]] | ||
| Zeile 39: | Zeile 39: | ||
=== Umfang Quadrat === | ==== Umfang Quadrat ==== | ||
[[Datei:Umfang Quadrat.png|thumb||left]] | [[Datei:Umfang Quadrat.png|thumb||left]] | ||
| Zeile 67: | Zeile 67: | ||
=== Umfang Dreieck === | ==== Umfang Dreieck ==== | ||
[[Datei:Umfang Dreieck NEU.png|thumb||left]] | [[Datei:Umfang Dreieck NEU.png|thumb||left]] | ||
Version vom 17. Januar 2017, 18:46 Uhr
Der Umfang
Umfangsberechnung Ebener Figuren
Um den Umfang eines Vielecks zu berechnen, musst du alle Seiten addieren.
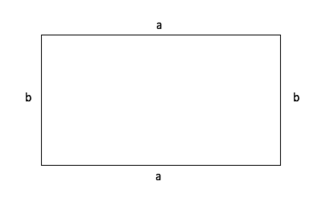
Umfang Rechteck
Umfang (U) = a + a + b + b
= 2 x a + 2 x b
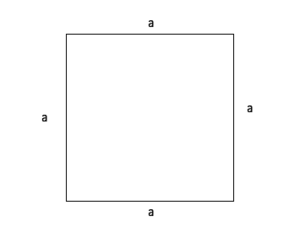
Umfang Quadrat
Umfang (U) = a + a + a + a
= 4 x a
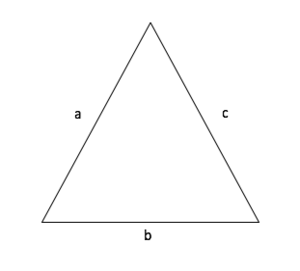
Umfang Dreieck
Umfang (U) = a + b + c