Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Umfang: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
== '''Der Umfang''' == | == '''Der Umfang''' == | ||
[[Datei:Bildschirmfoto Umfang.png|thumb||right | [[Datei:Bildschirmfoto Umfang.png|thumb||right] | ||
Der Umfang beschreibt die Länge der Außenlinie die eine Form, einen Gegenstand oder eine mathematische Figur umfasst. <br /> | Der Umfang beschreibt die Länge der Außenlinie die eine Form, einen Gegenstand oder eine mathematische Figur umfasst. <br /> | ||
| Zeile 28: | Zeile 28: | ||
==== Umfang Dreieck ==== | ==== Umfang Dreieck ==== | ||
[[Datei:Umfang Dreieck NEU.png|thumb||250px| | [[Datei:Umfang Dreieck NEU.png|thumb||250px|center]] | ||
| Zeile 51: | Zeile 51: | ||
==== Umfang Rechteck ==== | ==== Umfang Rechteck ==== | ||
[[Datei:Umfang Rechteck.png|thumb||300px| | [[Datei:Umfang Rechteck.png|thumb||300px|right]] | ||
| Zeile 73: | Zeile 73: | ||
==== Umfang Quadrat ==== | ==== Umfang Quadrat ==== | ||
[[Datei:Umfang Quadrat.png|thumb||280px| | [[Datei:Umfang Quadrat.png|thumb||280px|right]] | ||
| Zeile 104: | Zeile 104: | ||
==== Umfang beliebiges Vieleck ==== | ==== Umfang beliebiges Vieleck ==== | ||
[[Datei:Umfang Vieleck.png|thumb|| | [[Datei:Umfang Vieleck.png|thumb||right|250px]] | ||
Version vom 24. Januar 2017, 16:37 Uhr
Der Umfang
[[Datei:Bildschirmfoto Umfang.png|thumb||right]
Der Umfang beschreibt die Länge der Außenlinie die eine Form, einen Gegenstand oder eine mathematische Figur umfasst.
Legt man ein Maßband um einen Gegenstand und liest das Ergebnis ab, so hat man den Umfang des Gegenstands.
Meistens wird der Umfang berechnet, da das Messen nicht immer genau ist.
Umfangsberechnung Ebener Figuren
Sehr häufig hat man es in der Mathematik mit ebenen Figuren zu tun.
Für die Berechnung des Umfangs einer ebenen Figur muss man die Länge aller Seiten kennen.
Die Summe aller Seiten ergibt den Umfang, man muss sie also alle addieren um den Umfang zu erhalten.
Für die Berechnung des Umfangs der ebenen Figuren gibt es Formeln, welche alle das Prinzip der Summe aller Seiten beinhalten.
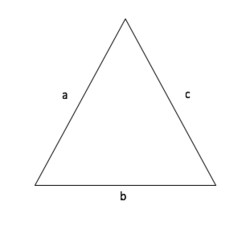
Umfang Dreieck
Umfang (U) = a + b + c
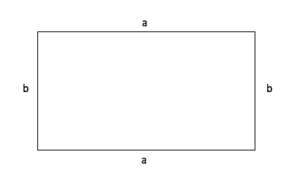
Umfang Rechteck
Umfang (U) = a + a + b + b
= 2 x a + 2 x b
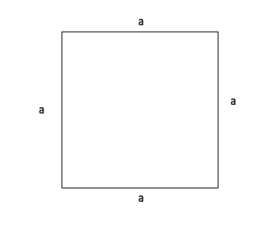
Umfang Quadrat
Umfang (U) = a + a + a + a
= 4 x a
Es gibt natürlich noch viele weitere ebene Figuren. Das Prinzip zur Berechnung des Umfangs ist aber immer das Selbe. Eine Ausnahme bildet hier nur der Kreis.
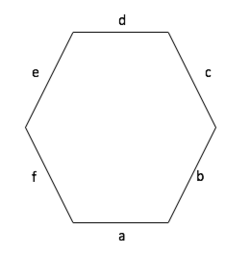
Umfang beliebiges Vieleck
Umfang (U) = a + b + c + d + e + f