Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Teiler: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 6: | Zeile 6: | ||
==== Beispiel ==== | ==== Beispiel ==== | ||
Wenn man zum Beispiel 12 [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Division|geteilt]] durch 3 | Wenn man zum Beispiel 12 [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Division|geteilt]] durch 3 teilt, ist das Ergebnis 4. Es bleibt kein Rest bestehen. Somit ist 3 ein Teiler von 12. | ||
Man schreibt auch ''' | Man schreibt auch '''3 | 12'''. | ||
| Zeile 30: | Zeile 30: | ||
== '''Gemeinsame Teiler''' == | == '''Gemeinsame Teiler''' == | ||
| Zeile 39: | Zeile 37: | ||
Die Zahlen, die man in beiden Teilermengen finden kann, sind die '''gemeinsamen Teiler.''' Hier wären das 1, 2 und 4. | Man kann auch die '''gemeinsamen Teiler''' von Zahlen bestimmen. | ||
In diesem Beispiel werden zwei Teilermengen angeschaut, die 12 und die 16. Die Zahlen, die man in beiden Teilermengen finden kann, sind die '''gemeinsamen Teiler.''' Hier wären das 1, 2 und 4. | |||
Mathematische würde man das so schreiben: | Mathematische würde man das so schreiben: | ||
:T<sub>12</sub> | :T<sub>12</sub> U T<sub>16</sub> = {1; 2; 4} | ||
Das Symbol | Das Symbol U zwischen den beiden Mengen zeigt an, dass nur die Schnittmenge betrachtet werden soll. Das heißt, dass die gemeinsamen Teiler zusammen aufgeschrieben werden. Die Zahlen, die nicht in beiden Teilermengen zu finden sind, werden weggelassen. | ||
Wenn zwei Zahlen keinen gemeinsamen Teiler außer der 1 haben, sind sie '''teilerfremd'''. | Wenn zwei Zahlen keinen gemeinsamen Teiler außer der 1 haben, sind sie '''teilerfremd'''. | ||
Zum Beispiel 5 und 7, denn | |||
:T<sub>5</sub> U T<sub>7</sub> = {1} | |||
Version vom 19. Februar 2017, 19:03 Uhr
Teiler
Teiler sind Zahlen, die eine besondere Beziehung zu anderen Zahlen haben.
Wenn man eine Zahl durch diesen Teiler dividiert, bleibt kein Rest übrig. Jede Zahl hat mehrere Teiler. Mathematisch nennt man den Teiler auch Divisor.
Beispiel
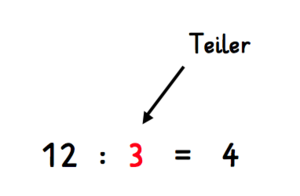
Wenn man zum Beispiel 12 geteilt durch 3 teilt, ist das Ergebnis 4. Es bleibt kein Rest bestehen. Somit ist 3 ein Teiler von 12. Man schreibt auch 3 | 12.
Teilermenge
12 hat nicht nur die Zahl 3 als Teiler. Sie ist außerdem durch 1, 2, 4, 6 und 12 ohne Rest teilbar.
Die Menge aller Teiler einer Zahl nennt man Teilermenge. Die Teilermenge von 12 beinhaltet also 1, 2, 3, 4, 6 und 12. Man schreibt das auch so:
- T12 = {1; 2; 3; 4; 6; 12}
Das T steht für die Teilermenge. Die kleine 12 daneben zeigt einem die Zahl, deren Teilermenge man sucht. Die Zahlen in den geschweiften Klammern {...} sind alle Zahlen, die Teiler von 12 sind.
Eine Teilermenge ist nicht unendlich, das heißt es gibt immer eine genaue Anzahl von Teilern einer Zahl. Außerdem sind in jeder Teilermenge mindestens die Zahl selbst und die 1 enthalten.
Es gibt auch Zahlen, die nur durch sich selbst und die 1 als Teiler haben. Diese Zahlen nennt man dann Primzahlen.
Gemeinsame Teiler
- T12 = {1; 2; 3; 4; 6; 12}
- T16 = {1; 2; 4; 8; 16}
Man kann auch die gemeinsamen Teiler von Zahlen bestimmen.
In diesem Beispiel werden zwei Teilermengen angeschaut, die 12 und die 16. Die Zahlen, die man in beiden Teilermengen finden kann, sind die gemeinsamen Teiler. Hier wären das 1, 2 und 4.
Mathematische würde man das so schreiben:
- T12 U T16 = {1; 2; 4}
Das Symbol U zwischen den beiden Mengen zeigt an, dass nur die Schnittmenge betrachtet werden soll. Das heißt, dass die gemeinsamen Teiler zusammen aufgeschrieben werden. Die Zahlen, die nicht in beiden Teilermengen zu finden sind, werden weggelassen.
Wenn zwei Zahlen keinen gemeinsamen Teiler außer der 1 haben, sind sie teilerfremd. Zum Beispiel 5 und 7, denn
- T5 U T7 = {1}
Größter gemeinsamer Teiler
Der größte gemeinsame Teiler ist die größte Zahl, die in einer gemeinsamen Teilermenge von zwei Zahlen zu finden ist. In dem Beispiel T12 ∩ T16 wäre das die 4.
- T12 ∩ T16 = {1; 2; 4}