Knobeln mit Mieze Mia: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
|||
| (10 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
"Knobeln mit Mieze Mia" ist eine gemeinschaftliche entwickelte Knobelkartei unter offener Nutzungslizenz. | |||
'''Gemeinschaftlich entwickelt'''<br /> | |||
Zur Knobelkartei werden alle Quelldateien mitveröffentlich. Daher sind alle interessierten Nutzer aufgerufen, an der Weiterentwicklung der Kartei mitzuwirken. Vorschläge für neue Aufgaben können auf dieser Seite eingereicht werden. Dabei spielt es keine Rolle, ob die Aufgaben schon die Vorlage eingefügt sind oder nur als Text in der Mail umschrieben werden. | |||
'''Offene Nutzungslizenz'''<br /> | |||
Die Aufgaben und Materialien der Knobelkartei sind unter einer creative-commons-Lizenz veröffentlicht. Dies ermöglicht allen Nutzern folgende Rechte | |||
*Teilen — das Material in jedwedem Format oder Medium vervielfältigen und weiterverbreiten | |||
*Bearbeiten — das Material remixen, verändern und darauf aufbauen und zwar für beliebige Zwecke, sogar kommerziell. | |||
Der Lizenzgeber kann diese Freiheiten nicht widerrufen solange Sie sich an die Lizenzbedingungen halten. | |||
Dabei geltende folgende Bedingungen: | |||
*Namensnennung — Sie müssen angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade Sie oder Ihre Nutzung besonders. | |||
*Weitergabe unter gleichen Bedingungen — Wenn Sie das Material remixen, verändern oder anderweitig direkt darauf aufbauen, dürfen Sie Ihre Beiträge nur unter derselben Lizenz wie das Original verbreiten. | |||
Vollständiger Lizenztext unter: https://creativecommons.org/licenses/by-sa/4.0/legalcode.de | |||
Sowohl die PDF-Dateien, als auch die Quelldateien, als auch die Bilddateien dürfen (und sollen) z.B. auf Schulhomepages oder an anderer Stelle veröffentlicht werden. | |||
==Überlegungen zum Einsatz im Unterricht== | ==Überlegungen zum Einsatz im Unterricht== | ||
Um die noch immer stetig wachsende Knobelkartei im Unterricht zu nutzen, gibt es verschiedene Möglichkeiten. Hier kommt ein erster Vorschlag: | Um die noch immer stetig wachsende Knobelkartei im Unterricht zu nutzen, gibt es verschiedene Möglichkeiten. Hier kommt ein erster Vorschlag: | ||
| Zeile 5: | Zeile 26: | ||
Die Etiketten kann man (ggf. schon geschnitten) in einem Karteikasten o.ä. bereitstellen. Die Schüler*innen können sich dann (in Freiarbeitsphasen etc.) ein Etikett nehmen und dies in ihr Heftchen einkleben, um dann individuell an der Aufgabe zu arbeiten. | Die Etiketten kann man (ggf. schon geschnitten) in einem Karteikasten o.ä. bereitstellen. Die Schüler*innen können sich dann (in Freiarbeitsphasen etc.) ein Etikett nehmen und dies in ihr Heftchen einkleben, um dann individuell an der Aufgabe zu arbeiten. | ||
==Twitterkanal== | |||
tbc. | |||
==Aufgaben Klasse 3/4== | ==Aufgaben Klasse 3/4== | ||
===Aufgabe 1-10=== | |||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
! Aufgabe !! Lehrerkommentar !! PDF-Vorlage | !Aufgabe!!Lehrerkommentar!!PDF-Vorlage | ||
|- | |- | ||
| [[Datei:Knobelkartei - A1.png|miniatur]] || Diese kombinatorische Aufgabe ist vergleichsweise einfach zu lösen. Für den ersten Würfel gibt es 6 verschiedene Möglichkeiten zu fallen (1 - 6), für den zweiten Würfel ebenfalls. Demnach gäbe es eigentlich 6 · 6 = 36 Möglichkeiten. Hier greift jedoch die Einschränkung, dass nur verschiedene Würfelergebnisse gezählt werden sollen. Die Ergebnisse "1 und 6", sowie "6 und 1" sind in diesem Sinne identisch und werden als ein Ergebnis gewertet. Somit bleiben 21 verschiedene Möglichkeiten übrig: | |[[Datei:Knobelkartei - A1.png|miniatur]]||Diese kombinatorische Aufgabe ist vergleichsweise einfach zu lösen. Für den ersten Würfel gibt es 6 verschiedene Möglichkeiten zu fallen (1 - 6), für den zweiten Würfel ebenfalls. Demnach gäbe es eigentlich 6 · 6 = 36 Möglichkeiten. Hier greift jedoch die Einschränkung, dass nur verschiedene Würfelergebnisse gezählt werden sollen. Die Ergebnisse "1 und 6", sowie "6 und 1" sind in diesem Sinne identisch und werden als ein Ergebnis gewertet. Somit bleiben 21 verschiedene Möglichkeiten übrig: | ||
1 + 1; 1 + 2; 1 + 3; 1 + 4; 1 + 5; 1 + 6; 2 + 2; 2 + 3; 2 + 4; 2 + 5; 2 + 6; 3 + 3; 3 + 4; 3 + 5; 3 + 6; 4 + 4; 4 + 5; 4 + 6; 5 + 5; 5 + 6; 6 + 6 | 1 + 1; 1 + 2; 1 + 3; 1 + 4; 1 + 5; 1 + 6; 2 + 2; 2 + 3; 2 + 4; 2 + 5; 2 + 6; 3 + 3; 3 + 4; 3 + 5; 3 + 6; 4 + 4; 4 + 5; 4 + 6; 5 + 5; 5 + 6; 6 + 6 | ||
Die Schülerinnen und Schüler werden am ehesten mit einem strukturierten Vorgehen auf die vollständige Lösung kommen: Erst alle Würfelergebnisse mit 1, dann alle Würfelergebnisse mit 2, ..., am Ende alle doppelten Ergebnisse streichen. In diese Richtung könnten auch mögliche Hilfestellungen gehen. | Die Schülerinnen und Schüler werden am ehesten mit einem strukturierten Vorgehen auf die vollständige Lösung kommen: Erst alle Würfelergebnisse mit 1, dann alle Würfelergebnisse mit 2, ..., am Ende alle doppelten Ergebnisse streichen. In diese Richtung könnten auch mögliche Hilfestellungen gehen. | ||
|| [[Datei:Knobelkartei- | ||[//grundschullernportal.zum.de/images/0/05/Knobelkartei-A1.pdf Download] | ||
|- | |||
|[[Datei:Knobelkartei - A2.png|miniatur]]||Diese geometrische Aufgabe lässt sich auf zwei Weisen lösen: kopfgeometrisch, indem man sich den Faltvorgang vorstellt oder enakitv, indem die Faltvorlagen ausgeschnitten und zusammengefaltet werden. | |||
Falsch ist jedenfalls die Vorlage 3, denn die beide Flächen ganz rechts überdecken sich beim Falten, so dass der entstehende Würfel an einer Seite offen ist. | |||
||[//grundschullernportal.zum.de/images/1/14/Knobelkartei-A2.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A3.png|miniatur]]||Diese Aufgabe gehört im Grunde in die Kategorien Arithmetik und Kombinatorik. Gesucht wird eine vierstellige Zahl. Bei der Beschreibung wurde bewusst auf die Verwendung der Stellenwertbezeichnungen (Einer, Hunderter, ...) verzichtet, da Nummern eines Fahrradschloss in der Regel als Set von Einzelziffern ausgesprochen werden. Bei der Lösung empfiehlt es sich, von der dritten Stellen ausgehend zu überlegen und dann nach und nach zu überlegen, was daraus für die zweite und erste Stelle folgt: | |||
Dritte Stelle '''1''' -> Zweite Stelle '''2''' -> Erste Stelle '''4''' | |||
Dritte Stelle '''2''' -> Zweite Stelle '''4''' -> Erste Stelle '''6''' | |||
Dritte Stelle '''3''' -> Zweite Stelle '''6''' -> Erste Stelle '''8''' | |||
Dritte Stelle '''4''' -> Zweite Stelle '''8''' -> Erste Stelle '''10 -> nicht möglich''' | |||
An vierter Stelle kann nur eine ungerade Ziffer stehen (1, 3, 5, 7, 9). Da es die Zusatzbedingung gibt, dass eine Ziffer in der Geheimnummer doppelt vorkommen muss, ergeben sich folgende Möglichkeiten: | |||
{| class="wikitable" | |||
|1. Stelle | |||
|2. Stelle | |||
|3. Stelle | |||
|4. Stelle | |||
|- | |||
|4 | |||
|2 | |||
|1 | |||
|1 | |||
|- | |||
|6 | |||
|4 | |||
|2 | |||
|nicht möglich | |||
|- | |||
|8 | |||
|6 | |||
|3 | |||
|3 | |||
|} | |||
Es gibt also zwei verschiedene Möglichkeiten, die Mia ausprobieren müsste. | |||
||[//grundschullernportal.zum.de/images/2/2f/Knobelkartei-A3.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A4.png|miniatur]]||Da schon bekannt ist, dass "ZeigeLinks" = 2 ist, kann man über die Berechnung der Einerstelle ("DaumenRunter" · "ZeigeLinks" = 2) ermitteln, dass "DaumenRunter" = 1 sein muss. Als nächstes schaut man sich die Berechnung der Hunderterstelle an ("ZeigeRechts" · "ZeigeLinks" = 2) Da man schon weiß, dass "ZeigeLinks" = 2 ist, muss also "ZeigeRechts" = 6 sein. Wenn man danach zur Zehnerstelle zurückgeht, weiß man auch, dass "DaumenHoch" = 3 ist, denn sonst würde die dazugehörende Rechnung "DaumenHoch" · "ZeigeLinks" = 6 nicht zu lösen sein. Bleibt noch die Rechnung der Tausenderstelle: "Victory" · "Victory" = 11. Von der Rechnung der Hunderterstelle haben wir noch einen Übertrag übrig. Daher muss "Victory" = 5 sein, damit die Rechnung aufgehen kann. | |||
Die vollständig gelöste Rechnung lautet dann: 5631 · 2 = 11262 | |||
||[//grundschullernportal.zum.de/images/1/17/Knobelkartei-A4.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A5.png|miniatur]]||Bei dieser Aufgabe steht vor allem die Frage im Vordergrund, welche Rechnung in welcher Reihenfolge durchgeführt werden - und was am Ende mit den Einzelergebnissen gemacht werden muss. Tipps an die Schüler könnten also vor allem in diese Richtung gehen. | |||
Da Mia 54 Bonbons geschenkt bekommen hat, 7 Bonbons aber selbst essen möchte, bleiben ihr zum Verteilen nur noch 47 Stück. | |||
8 + 7 · 3 + 4 = 33 Bonbons werden an eine fest vorgegebene Zahl von 16 Freunden verteilt. | |||
Es bleiben also 14 Bonbons übrig, die sie an "den Rest" verteilt, jeweils 2 Bonbons pro Kind. Somit werden diese 14 Bonbons also an 7 Kinder verteilt. | |||
Insgesamt verteilt Mia ihre Bonbons also an 23 Freunde - und sich selbst. | |||
||[//grundschullernportal.zum.de/images/2/26/Knobelkartei-A5.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A6.png|miniatur]]||Für die richtige Lösung dieser Aufgabe ist eine Skizze hilfreich. Daher sind direkt unter der Aufgabe die 4 Wegpunkte des 2,6 km langen Weges dargestellt. | |||
Zuerst lässt sich recht einfach bestimmen, wie weit der Weg von Momo zum Spielplatz ist: Wenn Mia zu Momo geht, legt sie 2,6 km zurück. Geht sie jedoch nur bis zum Spielplatz, dann ist der 2,08 km lang. Also muss der Weg vom Spielplatz zu Momo 2,6 km - 2,08 km = 0,052 km lang sein. | |||
Geht nun Momo bis zur Kirche, dann ist sein Weg 700 m lang. Zieht man hiervon nun die Wegstrecke ab, die er erstmal bis zum Spielplatz geht, dann erhält man als Ergebnis die Wegstrecke vom Spielplatz bis zur Kirche. 700 m - 520 m = 180 m. Spielplatz und Kirche liegen also nur 180 m auseinander. | |||
||[//grundschullernportal.zum.de/images/b/bf/Knobelkartei-A6.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A7.png|miniatur]]||Als Hilfsmittel für die Lösung dieser Aufgabe bietet sich eine Rechentabelle an. Beim Ausfüllen der Tabelle ist jedoch zu beachten, dass der Zuwachs beim Schal nicht in gleichen Schritten erfolgt, sondern Mia jeden Tag ein bisschen mehr schafft, weil sie mehr Übung beim Stricken hat. Dies sprachlich zu erfassen und bei der Rechnung umzusetzen, dürfte für die Kinder die größte Hürde sein. An dieser Stelle könnten also erste Tipps ansetzen (neben dem Hinweis auf die Verwendung einer Rechentabelle). | |||
{| class="wikitable" | |||
|'''Wochentag''' | |||
|'''Zuwachs''' | |||
|'''Neue Länge''' | |||
|- | |||
|Montag | |||
|37 cm | |||
|37 cm | |||
|- | |||
|Dienstag | |||
|51 cm | |||
|88 cm | |||
|- | |||
|Mittwoch | |||
|65 cm | |||
|153 cm | |||
|- | |||
|Donnerstag | |||
|79 cm | |||
|232 cm | |||
|- | |||
|Freitag | |||
|93 cm | |||
|325 cm | |||
|} | |||
Da Mias Schal 250 cm lang werden soll, wird sie ihren Schal erst am Freitag fertiggestellt haben. | |||
||[//grundschullernportal.zum.de/images/9/96/Knobelkartei-A7.pdf Download] | |||
|- | |||
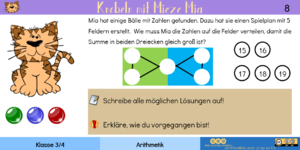
|[[Datei:Knobelkartei - A8.png|miniatur]]||Die Lösung der Aufgabe wir etwas einfacher, wenn sich im ersten Schritt überlegt, welche Bälle/Zahlen überhaupt nur für das mittlere Feld in Frage kommen. Die Zahlen 16 und 18 scheiden hierbei aus, da die Summe der verbleibenden 4 Bälle dann ungerade wird. Eine ungerade Summe lässt sich jedoch nicht gleichmäßig auf beide Quadrate verteilen. | |||
Somit ergeben sich folgende Möglichkeiten: | |||
{| class="wikitable" | |||
|'''Links''' | |||
|'''Mitte''' | |||
|'''Rechts''' | |||
|- | |||
|17,18 | |||
|15 | |||
|16,19 | |||
|- | |||
|15,19 | |||
|17 | |||
|16,18 | |||
|- | |||
|15,18 | |||
|19 | |||
|16,17 | |||
|} | |||
Diese drei Lösungen lassen sich natürlich gespiegelt aufschreiben, wodurch es 6 Lösungen gäbe. Zudem gibt es für jede Lösung noch 4 verschiedene Varianten, die 4 Bälle auf die Felder zu verteilen. Dann wären es sogar 24 verschiedene Möglichkeiten. Hier kann jedoch im Gespräch mit den Schülern besprochen werden, ob diese Varianten jeweils als verschiedene oder identische Lösung gewertet werden sollen. | |||
||[//grundschullernportal.zum.de/images/6/6d/Knobelkartei-A8.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A9.png|miniatur]]||Um die Länge der Leine zu ermitteln, muss man zuerst die Einzellängen der Wäschestücke mit den jeweiligen Breiten multiplizieren. Die 4 Bettlaken sind 3,8m breit, die T-Shirts 2,1m. Die 10 Socken sind zusammen 1,20m breit. Somit ergibt sich schonmal eine Gesamtbreite von 7,1 m. Insgesamt sind es 20 Wäschstücke, so dass es 19 Zwischenräume á 10cm gibt, was dann in der Summe 1,90m Zwischenraum ergibt. Die Wäscheleine sollte also mindesten 9m lang sein. | |||
||[//grundschullernportal.zum.de/images/5/58/Knobelkartei-A9.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A10.png|miniatur]]||Einen echten Lösungsweg gibt zu dieser Aufgabe nicht, da die Aufgabe idealerweise kopfgeometrisch gelöst wird. Bei mentalen Auseinanderbauen des Quaders wird man feststellen, dass sich in der 2. und 3. Schicht in der Mitte je ein Würfel befindet, der keinen Außenkontakt hat. Diese beiden Würfel werden folglich auch nicht angemalt, wenn Mia den großen Quader von außen bemalt. Folglich hat Momo mit seiner Aussage nicht recht. | |||
||[//grundschullernportal.zum.de/images/7/72/Knobelkartei-A10.pdf Download] | |||
|} | |||
===Aufgabe 11-20=== | |||
{| class="wikitable" | |||
|- | |||
!Aufgabe!!Lehrerkommentar!!PDF-Vorlage | |||
|- | |||
|[[Datei:Knobelkartei - A11.png|miniatur]]||Die Rechnungen hinter dieser Rechengeschichte sind (mathematisch betrachtet) zwei Gleichungen mit zwei Unbekannten: 2€ + 6 Spiele + 3 Hosen = 35€ und 4€ + 7 Spiele + 2 Hosen = 35€. Man könnte jetzt für "Spiele" und "Hosen" Variablen einsetzen, eine gleichen nach "Hosen" auflösen und dann in die zweite Gleichung einsetzen. Dann erhielte man als Lösung: ein Spiel kostet 3€ und eine Hose kostet 5€. | |||
Die Schülerinnen und Schüler werden vermutlich nicht mit Variablen arbeiten. Hier hilft vermutlich systematisches Ausprobieren: einen Betrag für das Spiel annehmen, mit Hilfe des ersten Satzes ausprobieren, was dann die Hose kosten muss und diese Werte dann an der zweiten Gleichung überprüfen. | |||
||[//grundschullernportal.zum.de/images/a/a7/Knobelkartei-A11.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A12.png|miniatur]]||Um die Fairness dieses Würfelspiels einschätzen zu können, muss man die Wahrscheinlichkeiten der beiden Ereignisse bestimmen und auswerten. Beim Würfeln mit zwei Würfeln gibt es 6 · 6 = 36 Möglichkeiten, wie die Würfel fallen können. Hierbei sind es jedoch nur 9 Kombinationen, in denen das Produkt der beiden Zahlen auf den Würfeln ungerade ist: 1 · 1; 1 · 3; 1 · 5; 3 · 1; 3 · 3; 3 · 5; 5 · 1; 5 · 3; 5 · 5. In allen anderen Würfelkonstellationen ist die Zahl mindestens eines Würfels gerade, wodurch auch das Produkt gerade ist. Das Würfelprodukt ist also in 27 von 36 Fällen gerade, was eine Gewinnchance von 75% ergibt. Das Spiel ist also tatsächlich unfair. | |||
||[//grundschullernportal.zum.de/images/e/ec/Knobelkartei-A12.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A13.png|miniatur]]|| | |||
Die Tabelle gibt wieder, welche Zahlen mit welcher Kombination möglich sind. Wichtig: Mia kann natürlich auch (absichtlich) vorbeiwerfen! In der Tabelle ist dies mit einem X gekennzeichnet | |||
{| class="wikitable" | |||
|'''Wurf 1''' | |||
|'''Wurf 2''' | |||
|'''Wurf 3''' | |||
|'''Summe''' | |||
|- | |||
|9 | |||
|1 | |||
|X | |||
|10 | |||
|- | |||
|9 | |||
|1 | |||
|1 | |||
|11 | |||
|- | |||
|12 | |||
|X | |||
|X | |||
|12 | |||
|- | |||
|12 | |||
|1 | |||
|X | |||
|13 | |||
|- | |||
|12 | |||
|1 | |||
|1 | |||
|14 | |||
|- | |||
|9 | |||
|6 | |||
|X | |||
|15 | |||
|- | |||
|9 | |||
|6 | |||
|1 | |||
|16 | |||
|- | |||
| colspan="3" |nicht möglich | |||
|17 | |||
|- | |||
|12 | |||
|6 | |||
|X | |||
|18 | |||
|- | |||
|12 | |||
|6 | |||
|1 | |||
|19 | |||
|- | |||
| colspan="3" |nicht möglich | |||
|20 | |||
|- | |||
|12 | |||
|9 | |||
|X | |||
|21 | |||
|- | |||
|12 | |||
|9 | |||
|1 | |||
|22 | |||
|- | |||
| colspan="3" |nicht möglich | |||
|23 | |||
|- | |||
|9 | |||
|9 | |||
|6 | |||
|24 | |||
|- | |||
|12 | |||
|12 | |||
|1 | |||
|25 | |||
|} | |} | ||
||[//grundschullernportal.zum.de/images/9/94/Knobelkartei-A13.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A14.png|miniatur]]||Diese Aufgabe ist (vielleicht) die Mutter aller Knobelaufgaben. Laut Wikipedia ist sie schon seit fast 900 Jahren bekannt. Die Lösung wird in der Wikipedia folgendermaßen beschrieben: | |||
Zunächst füllt man das 5-Liter-Gefäß aus dem 8-Liter-Gefäß bis zum Rand, zurück bleiben 3 Liter: (0, 5, 3) | |||
Aus dem 5-Liter-Gefäß füllt man das 3-Liter-Gefäß bis zum Rand: (3, 2, 3) | |||
Das 3-Liter-Gefäß entleert man in das 8-Liter-Gefäß: (0, 2, 6) | |||
Den Inhalt des 5-Liter-Gefäßes schüttet man in das 3-Liter-Gefäß: (2, 0, 6) | |||
Man füllt das 5-Liter-Gefäß erneut aus dem 8-Liter-Gefäß: (2, 5, 1) | |||
Man füllt das 3-Liter-Gefäß aus dem 5-Liter-Gefäß auf: (3, 4, 1) | |||
Man schüttet den Inhalt des 3-Liter-Gefäßes in das 8-Liter-Gefäß zurück: (0, 4, 4) | |||
Zu der Knobelaufgabe gibt es auch eine Internetseite, mit der man den Prozess durch Ausprobieren lösen kann: http://www.ablmcc.edu.hk/~scy/home/javascript/notes/jugs/ | |||
||[//grundschullernportal.zum.de/images/0/07/Knobelkartei-A14.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A15.png|miniatur]]||Um die Gewichte der einzelnen Obstsorten ermitteln zu können, hilft es, wenn man sich als erstes die beiden oberen "Gleichungen" ansieht und überlegt, was der Unterschied zwischen den beiden Zeilen ist. In der unteren Zeile gibt es einen Apfel mehr, wodurch das Gewicht um 510g - 330g =180g steigt. Somit wiegt ein Apfel 180g. Daraus ergibt sich direkt, dass eine Birne 300g - 180g = 150g wiegen muss. | |||
Eine Melone und eine Birne (150g) wiegen 5 · 180g = 900g. Von den 900g muss man also 150g abziehen, um zu ermitteln, dass eine Melone 750g wiegt. | |||
||[//grundschullernportal.zum.de/images/f/ff/Knobelkartei-A15.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A16.png|miniatur]]||Da Mia nur in 4er-Schritten die Treppe hinaufspringen kann, wird sie nicht auf direktem Weg zu Momo kommen. Sie muss zuerst auf eine Stufe oberhalb Momo springen, die an der Einerstelle entweder eine 7 oder eine 2 stehen hat. In 4er Schritten wird sie aber nicht auf eine Stufe kommen, deren Einerstelle "7" ist. | |||
Der kürzeste Weg geht in 8 Sprüngen auf Stufe 32 und dann in 2 Sprüngen herunter auf die 22. Sie braucht also 10 Sprünge. | |||
||[//grundschullernportal.zum.de/images/e/e0/Knobelkartei-A16.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A17.png|miniatur]]||Da sich die Zahl der Wespen in jeder Woche verdoppelt hat, muss man zur Ermittlung des Baubeginns einfach rückwärts rechnen, also so oft die Zahl 768 halbieren, bis man bei der Zahl 6 ankommt. | |||
768 : 2 = 384 | |||
384 : 2 = 192 | |||
192 : 2 = 96 | |||
96 : 2 = 48 | |||
48 : 2 = 24 | |||
24 : 2 = 12 | |||
12 : 2 = 6 | |||
Der Nestbau hat folglich vor 7 Wochen begonnen. | |||
||[//grundschullernportal.zum.de/images/3/3b/Knobelkartei-A17.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A18.png|miniatur]]||Bei der Lösung der Aufgabe hilft es, wenn man sich in einem ersten Schritt überlegt, was überhaupt passiert, wenn eine Gruppe von 4 Leuten sich gegenseitig die Hände schüttelt: | |||
Person 1 schüttelt 3 Personen die Hände (sich selbst natürlich nicht) | |||
Person 2 schüttelt 2 Personen die Hände (mit Person 1 hatte sie bereits das Vergnügen | |||
Person 3 schüttelt 1 Person die Hände | |||
Person 4 hat schon mit jedem die Hände geschüttelt. | |||
Bei 4 Personen gibt es also 1 + 2 + 3 = 6 Schüttelvorgänge. Mit jeder Person, die dazukommt, muss nun eine weitere Zahl addiert werden. | |||
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = 78. Dies ist jedoch die Rechnung für 13 Personen. Auf der Party schütteln sich also 13 Katzen die Hände. Da Mia selbst auch dabei ist, müssen also 12 Freunde auf der Party eingeladen sein. | |||
||[//grundschullernportal.zum.de/images/2/27/Knobelkartei-A18.pdf Download] | |||
|- | |||
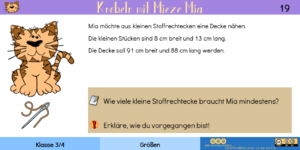
|[[Datei:Knobelkartei - A19.png|miniatur]]||Vorweg: Bei der Lösung wird außer Acht gelassen, dass die Stoffstücke beim Nähen der Decke ein wenig überlappen sollten. Es muss also nur ein Weg gefunden werden, wie die große Fläche von 91 cm x 88 cm mit den kleinen Stücken ausgelegt werden kann. Dabei müssen die Stücke natürlich nicht in der beschriebenen Ausrichtung vernäht werden, sondern dürfen auch gedreht werden. | |||
Für die lange Seite (91 cm) braucht man 8 Stücke mit 13 cm Breite. Für die kürzere Seite reichen dann 11 Stücke mit 8 cm Breite, so dass es insgesamt 88 Stücke Stoff sind. | |||
||[//grundschullernportal.zum.de/images/c/c3/Knobelkartei-A19.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A20.png|miniatur]]||Am sichersten löst man diese AUfgabe natürlich, wenn man sich die Muster 1 bis 10 aufmalt und anschließend die Punkte/Erbsen auszählt. Dies dürfte jedoch einige Zeit in Anspruch nehmen. Schneller geht es, wenn man die arithmetische Regel für die Muster erkennt. Muster 1 besteht aus 1 · 2 Erbsen, Muster 2 aus 2 · 3 Erbsen usw. Muster 10 wird also aus 10 · 11 Erbsen bestehen. Demnach braucht Mia für ihre Muster insgesamt 440 Erbsen (2 + 6 + 12 + 20 + 30 + 42 + 56 + 72 + 90 + 110). | |||
||[//grundschullernportal.zum.de/images/6/64/Knobelkartei-A20.pdf Download] | |||
|} | |||
===Aufgabe 21-20=== | |||
{| class="wikitable" | |||
|- | |||
!Aufgabe!!Lehrerkommentar!!PDF-Vorlage | |||
|- | |||
|[[Datei:Knobelkartei - A21.png|miniatur]]||Durch die Zeichnung ist diese Aufgabe relativ einfach zu lösen. Mit ihrer Hilfe lässt sich nämlich ermitteln, dass die Pyramide 8 Kanten besitzt, die alle gleich Lang sind. Für den Bau der Pyramide hat Mia 48 cm Draht (50 cm - 2 cm) verwendet. Folglich sind die Kanten 48 cm : 8 = 6 cm lang. Eine interessante Frage wäre nun, wie ich die Pyramide ist, aber für Grundschüler vermutlich nicht zu lösen :). | |||
||[//grundschullernportal.zum.de/images/f/f1/Knobelkartei-A21.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A22.png|miniatur]]||Intuitiv möchte man diese Aufgabe vielleicht mit einer Zeichnung lösen. Allerdings wird beim Betrachten des Ergebnisses klar, dass dies eine unverhältnismäßig aufwendige Aufgaben wird. Daher sind hier arithmetische Überlegungen die bessere Alternative: Da jeder der 6 dicken Äste 5 dicke Zweige hat, sind es 6 · 5 = 30 dicke Zweite, die der Baum hat. Jeder der dicken Zweige hat 4 dünne Zweige, was in der Summe 30 · 4 = 120 dünne Zweige hat. An jedem der Zweige hängen nur 2 Äpfel, was insgesamt 120 · 2 = 240 Äpfel sind. | |||
||[//grundschullernportal.zum.de/images/6/6a/Knobelkartei-A22.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A23.png|miniatur]]||Bei dieser Aufgabe geht es zu erst einmal darum, einen sinnvollen Ansatz für die Lösung zu finden. Hier ist eine Zeichnung hilfreich, die das Glockengeläut visualisiert. Um 7 Uhr wird die Glocke 7 Mal klingen, unterbrochen von 6 Pausen: O - O - O - O - O - O - O. | |||
Da das gesamte Läuten 24 Sekunden dauert, muss jede Pause (etwa) 6 Sekunden dauern. (An dieser lassen wir einmal außer Acht, dass auch der 7. Schlag noch nachklingen wird und jeder Schlag selbst auch eine Dauer von wenigen Millisekunden hat. | |||
Um 22 Uhr sieht die Visualisierung so aus: O - O - O - O - O - O - O - O - O - O - O - O - O - O - O - O - O - O - O - O - O - O, bzw. O - O - O - O - O - O - O - O - O - O, je nachdem ob man annimmt, dass die Kirchenuhr 22 mal schlägt oder eben nur 10 mal. Entsprechend gibt es dann 21 bzw. 9 Schlagpausen. Daraus ergibt sich, dass das gesamte Geläute 54 Sekunden bzw. 126 Sekunden, also 2 Minuten und 6 Sekunden dauern wird. | |||
||[//grundschullernportal.zum.de/images/7/71/Knobelkartei-A23.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A24.png|miniatur]]||Bei dieser Aufgaben werden die Kinder wohl vor allem Trial-and-Error-Strategien anwenden. Um die geforderten 2 Dreiecke und 2 Vierecke zu erhalten, muss der Kuchen einmal exakt auf der Diagonalen geschnitten werden, so dass man zwei Dreiecke erhält. Danach schneidet man einmal nicht durch die Diagonale, um zwei Dreiecke und zwei Vierecke zu erhalten (die dann natürlich keine Rechtecke oder Quadrate sind, aber das war ja auch nirgends gefordert). | |||
||[//grundschullernportal.zum.de/images/8/8e/Knobelkartei-A24.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A25.png|miniatur]]||Die Lösung dürfte den Schüler*innen am einfachsten gelingen, wenn sie sich überlegen, wie lange Momo braucht, um einen kompletten Sack zu verbrauchen. Hierzu braucht er 60 Tage. In dieser Zeit verbraucht Mia 2 Säcke, so dass die beiden insgesamt in 60 Tagen 3 Säcke verbrauchen. Folglich kommen sie mit einem Sack 60 Tage : 3 = 20 Tage aus. | |||
||[//grundschullernportal.zum.de/images/4/4f/Knobelkartei-A25.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A26.png|miniatur]]||Vorab zwei Lösungen: 123 + 45 - 67 + 8 - 9 = 100 und 123 - 45 - 67 + 89 = 100 | |||
Diese Aufgabe löst man vermutlich am ehesten mit systematischen Probieren. | |||
||[//grundschullernportal.zum.de/images/4/4a/Knobelkartei-A26.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A27.png|miniatur]]||Wenn man diese Aufgabe strukturiert angehen möchte, zerlegt man den Würfel am besten "mental" in kleinere Einheiten: | |||
Der Würfel besteht aus 9 Dreierstangen. | |||
An einer Dreierstange gibt es 2 Paare von Berührungsflächen, so dass Mia für eine Stange zwei Punkte setzen muss. | |||
Für eine Platte (3x3 Würfel) braucht man 3 Stangen (also sechs Punkte). Beim Verbinden von zwei Stangen berühren sich immer 3 Paare von Berührungsflächen, macht also weiter 6 Klebepunkte. Pro Platte müssen also 12 Punkte gesetzt werden. | |||
Der Würfel besteht aus 3 Platten, wodurch schon 36 Klebepunkte erreicht werden. Beim verbinden zweier Platten berühren sich immer 9 Paare von Berührungsflächen. Dadurch entstehen also insgesamt 18 weitere Klebepunkte. | |||
Mia muss als insgesamt 54 Punkte setzen. | |||
||[//grundschullernportal.zum.de/images/c/c4/Knobelkartei-A27.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A28.png|miniatur]]||Mit einer Skizze/Tabelle lässt sich diese Aufgabe recht einfach lösen. Es geht jedoch auch mit logischen Überlegungen. Der erste Streifen ist rot. Da der Schal aus 6 Farben besteht, die sich immer in der gleichen Reihenfolge wiederholen, wird auch das 7. und das 13. Feld rot sein. Demnach ist das 14. Feld orange. Hier macht Mia also ihre Pause. Der Reihe nach macht sie beim 15. Feld mit gelb weiter. | |||
||[//grundschullernportal.zum.de/images/0/08/Knobelkartei-A28.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A29.png|miniatur]]||Für diese Aufgabe bedarf es einer kleinen Vorüberlegung: Da Mia 52 Leckerlis besitzt, sie aber am Ende eines übrig behält, hat sie nur 51 Leckerlis an ihre Kaninchen verfüttert. Die Kinder werden nun vermutlich mit systematischem Probieren vorgehen. Als Lehrer kann man die Aufgabe mit einer kleinen Gleichung lösen. Das kleinste Kaninchen bekommt x Leckerlis. Jeder weiteres Tier bekommt je ein Stück mehr. Es ergibt sich folgende Gleichung: x + x + 1 + x + 2 + x + 3 + x + 4 x + 5 = 51. Zusammengefasst ergibt sich: 6x + 15 = 51. Folglich sind 6x = 36, also X =6. Das kleinste Kaninchen hat 6 Leckerlis erhalten. | |||
||[//grundschullernportal.zum.de/images/5/58/Knobelkartei-A29.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A30.png|miniatur]]||Für die Lösung der Aufgabe muss man zuerst ermitteln, was eine Kugel Eis kostet. Mia kann sich 3 Kugeln Eis leisten, behält sogar noch 20ct übrig. Bis zur nächsten Kugel fehlen ihr jedoch 40ct. Folglich muss eine Kugel Eis 60ct kosten. Die 3 Kugeln, die Mia sich leisten kann, kosten also 1,80€. Da sie 20ct übrig hat, hatte sie zu Beginn ihres Einkaufs 2€ bei sich. | |||
||[//grundschullernportal.zum.de/images/3/34/Knobelkartei-A30.pdf Download] | |||
|} | |||
===Aufgabe 31-40=== | |||
{| class="wikitable" | |||
|- | |||
!Aufgabe!!Lehrerkommentar!!PDF-Vorlage | |||
|- | |||
|[[Datei:Knobelkartei - A31.png|miniatur]]||Die Anordnung der Kinder ist bei dieser Aufgabe eigentlich egal, so verlockt die Kinder jedoch vielleicht zu Lösungswegen mit Skizze. Mathematisch ist hier eigentlich nur die Aufgabe 36 : 8 = 4 Rest 4 zu lösen. Da am Ende ein Rest von 4 Keksen bleibt, Mia diese aber brav weiter verteilt, bekommen also 4 Freunde 5 Kekse, während 4 weitere Freunde nur 4 Kekse erhalten. | |||
||[//grundschullernportal.zum.de/images/2/2a/Knobelkartei-A31.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A32.png|miniatur]]||Insgesamt gibt es eigentlich 4 · 3 · 2 · 1 = 24 Möglichkeiten, das Blumenkistchen zu bepflanzen. Allerdings möchte ja auf jeden Fall, dass die rote Tulpe von der lila und der gelben Tulpe eingerahmt ist. Ein Teil des Kistchens ist also G - R - L oder L - R - G. Die schwarze Tulpe kann nun entweder immer links oder rechts neben dieser Gruppe stehen. Es gibt also 2 · 2 = 4 Möglichkeiten, wie Mia ihr Kistchen gestalten kann. | |||
PS: Es gibt wirklich (fast) schwarze Tulpen: http://www.meinanzeiger.de/erfurt/natur/gibt-es-wirklich-schwarze-tulpen-d16233.html | |||
||[//grundschullernportal.zum.de/images/0/00/Knobelkartei-A32.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A33.png|miniatur]]||Der gesamte Turm besteht aus 3 · 3 · 7 = 63 Würfeln. Zerlegt man den Turm in seine 7 Schichten, stellt man fest, dass zwei verschiedene Arten von Schichten gibt: 4 Schichten, in denen es 5 weiße und 4 schwarze Würfel gibt und 3 Schichten, in denen es 4 weiße und 5 schwarze Würfel gibt. Somit erkennt man schnell, dass es 32 weiße Würfel und 31 schwarze Würfel sind, die Mia in ihrem Turm verwendet hat. | |||
||[//grundschullernportal.zum.de/images/0/00/Knobelkartei-A33.pdf Download] | |||
|- | |||
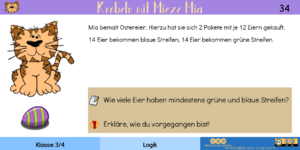
|[[Datei:Knobelkartei - A34.png|miniatur]]||Mia hat sich insgesamt 2 · 12 = 24 Eier gekauft. Da sie 14 Eier mit blauen Streifen versieht, bleiben vorerst 10 Eier "nackt". Wenn Mia nun in einem ersten Schritt zuerst diese 10 Eier mit grünen Streifen bemalt, muss sie dann aber noch 4 weitere Eier mit grünen Streifen versehen, die aber auch schon blaue Streifen haben. Es gibt also mindestens 4 zweifarbige Eier. | |||
||[//grundschullernportal.zum.de/images/8/80/Knobelkartei-A34.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A35.png|miniatur]]||Für die Lösung dieser Aufgabe ist es wichtig zu wissen, dass Dominosteine zwei Seiten haben und beim Legen einer Dominoreihe stets zwei gleiche Seiten aneinandergefügt werden. Folglich sind von den beiden leeren/geklauten Steinen schon zwei Felder bekannt (5 und 3). Die bisherige Gesamtsumme der Punkte beträgt inklusive dieser beiden Felder also 45. Da Mia bei der kompletten Reihe die Summe 47 gezählt hatte, müssen die beiden fehlenden Felder also jeweils mit einer 1 belegt werden. | |||
||[//grundschullernportal.zum.de/images/a/ac/Knobelkartei-A35.pdf Download] | |||
|- | |||
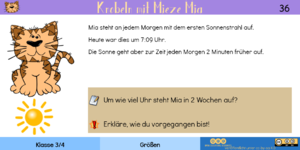
|[[Datei:Knobelkartei - A36.png|miniatur]]||Zwei Wochen haben 14 Tage. Somit wird die Sonne in 14 Tagen 28 Minuten früher aufgehen (die reale Veränderung der Sonnenaufgangszeiten ist leider nicht ganz im 2-Stunde-Rhythmus). Die Sonne geht demnach um 6:41 auf, was dann auch Mias Aufstehzeit entspricht. | |||
||[//grundschullernportal.zum.de/images/5/59/Knobelkartei-A36.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A37.png|miniatur]]||Die Kinder werden bei der Lösung ggf. zu einer Rechentabelle greifen oder die Taschengeldbeträge schrittweise zum Ausgangsbetrag addieren. Mit einer einfachen Überlegung gelingt die Lösung der Aufgabe jedoch viel einfacher: | |||
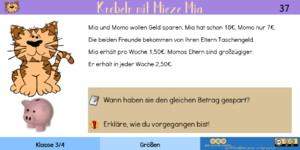
Mia hat zu Beginn 11€ mehr als Momo. Momo bekommt jedoch jede Woche 1€ mehr Taschengeld. Daher wird Mia ihren Vorsprung nach exakt 11 Wochen aufgebraucht haben. | |||
||[//grundschullernportal.zum.de/images/e/e2/Knobelkartei-A37.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A38.png|miniatur]]||Intuitiv wird man mit Sicherheit denken, dass es mit zwei Würfeln einfacher ist, die Würfelsumme 6 zu erreichen. Um zu erkennen, dass dem nicht so ist, sind einige Überlegungen nötig: | |||
Beim Würfeln mit zwei Würfeln gibt es 6 · 6 = 36 verschiedene Möglichkeiten, wie die Würfel fallen können. Davon gibt es aber nur 5 Möglichkeiten, die Summe 6 zu erreichen: 1 + 5; 2 + 4; 3 + 3; 4 + 2; 5 + 1. Die Chance beträgt als 5 von 36. Beim Würfeln mit nur einem Würfel beträgt die Chance für die 6 logischerweise 1 von 6 ... oder eben 6 von 36. Somit ist es wahrscheinlicher, mit einem Würfel die Würfelsumme 6 zu erreichen. | |||
||[//grundschullernportal.zum.de/images/e/e4/Knobelkartei-A38.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A39.png|miniatur]]||Bei dieser Aufgabe hilft es, wenn man sich im ersten Schritt überlegt, aus wie vielen Kugeln und Streichhölzern ein Würfel besteht. Es sind 8 Kugeln (Ecken) und 12 Streichhölzer (Kanten). Die fertige Figur besteht natürlich nicht aus 4 vollständigen Würfeln, sondern eigentlich nur aus 2 vollständigen Würfeln und einigen ergänzenden Bauteilen. Es sind insgesamt 20 Ecken (=Kugeln) und 36 Streichhölzer (=Kanten). | |||
||[//grundschullernportal.zum.de/images/8/8b/Knobelkartei-A39.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A40.png|miniatur]]||Mathematisch gesprochen soll eine Summe <=20 erzeugt werden, die aus möglichst vielen unterschiedlichen Summanden besteht. 1 + 2 + 3 + 4 + 5 = 15. Es bleiben zwar 5 Eier übrig, aber die Anzahl 5 hat Mia ja schon verteilt. Sie kann also höchstens 5 Nester füllen. | |||
Mit dieser Aufgabe geht die Knobelkartei in die Osterpause. Ab dem 24.04.2017 gibt es wieder neue Knobelaufgaben. Ich hoffe, dass ich die Kartei bis Jahresende auf 100 Aufgaben anwachsen lassen kann, ehe ich mich dann der Klasse 1/2 widmen kann. | |||
||[//grundschullernportal.zum.de/images/f/fc/Knobelkartei-A40.pdf Download] | |||
|} | |||
===Aufgabe 41-50=== | |||
{| class="wikitable" | |||
|- | |||
!Aufgabe!!Lehrerkommentar!!PDF-Vorlage | |||
|- | |||
|[[Datei:Knobelkartei - A41.png|miniatur]]||Mia muss bei ihrem Krankenhaus höchstens 10 Türen aufsuchen. Im ersten Stock sind es die Türen 103, 130, 112, und 121. Im zweiten Stock sind es die Türen 202, 220 und 211. Im dritten Stock dann noch die Türen 301 und 300. Und natürlich könnte die Großmutter auch in Zimmer 400 liegen. | |||
||[//grundschullernportal.zum.de/images/6/69/Knobelkartei-A41.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A42.png|miniatur]]||Aus mathematischer Sicht muss bei dieser Aufgabe eine ganzzahlige Zerlegung der Zahl 17 gefunden werden, bei der der erste Summand ein Vielfaches von drei ist und der zweite Summand ein Vielfaches von vier. Für die Lösung legt man sich am Besten eine Tabelle an, die die Vielfachen von drei auflistet: | |||
{| class="wikitable" | |||
|Vielfaches von 3 | |||
|Rest bis zur 17 | |||
|Vielfaches von 4? | |||
|- | |||
|3 | |||
|14 | |||
|nein | |||
|- | |||
|6 | |||
|11 | |||
|nein | |||
|- | |||
|9 | |||
|8 | |||
|ja | |||
|- | |||
|12 | |||
|5 | |||
|nein | |||
|- | |||
|15 | |||
|2 | |||
|nein | |||
|} | |||
Dann erkennt man schnell, dass Mia drei Dreiecke und zwei Vierecke gebaut haben muss! | |||
||[//grundschullernportal.zum.de/images/0/01/Knobelkartei-A42.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A43.png|miniatur]]||Die Lösung dieser Aufgabe gelingt eigentlich recht zügig und einfach. Man muss jedoch eine Besonderheit bedenken: Mia zählt 25 Autos bis zum Treffpunkt, Momo 31 Autos. Nun ist man geneigt schnell zu folgern, dass es insgesamt 25 + 31 = 56 Autos sind. Allerdings haben Mia und Momo das Auto ihres Treffpunktes doppelt gezählt. Es sind also insgesamt nur 56 - 1 = 55 Autos in der Schlange. | |||
||[//grundschullernportal.zum.de/images/2/26/Knobelkartei-A43.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A44.png|miniatur]]||Die Gartenarbeit von Mia lässt sich in eine einfache Gleichung übertragen: 3x + x = 52 (wobei X hierbei für die Anzahl der Möhren steht). Folglich sind 4x = 52 oder eben x = 13. | |||
Die Kinder werden vermutlich nicht auf die Idee kommen, eine Gleichung aufzustellen. In diesem Fall kann eine Rechentabelle helfen. | |||
||[//grundschullernportal.zum.de/images/4/4c/Knobelkartei-A44.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A45.png|miniatur]]||Um die Gesamtspieldauer des Hörbuchs zu ermitteln, muss mit Zeitangaben gerechnet werden, was für Kinder in der Regel ungewohnt ist, da hier nicht das Dezimale Stellenwertsystem ausgenutzt werden kann. | |||
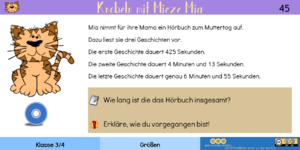
Die erste Geschichte hat eine Spieldauer von 425 Sekunden. Dies entspricht 7 Minuten und 5 Sekunden. Diese Dauer lässt sich geschickt mit der Dauer der dritten Geschichte addieren. Zusammen laufen diese beiden Geschichten für 14 Minuten. Addiert man hierzu noch die Länge der zweiten Geschichte, ergibt sich eine Gesamtspieldauer von 18 Minuten und 13 Sekunden. | |||
||[//grundschullernportal.zum.de/images/c/cc/Knobelkartei-A45.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A46.png|miniatur]]||Da Mia ein Jahr älter ist als Momo, wird Momo seinen 9. Geburtstag erst im Jahr 2018 feiern. Da Mia zudem noch 7 Tage älter ist, feiert Momo seinen Geburtstag auch 7 Tage später, also am 9.5.2018. Das Hauptproblem für die Kinde dürfte sein, in welche Richtung man denken/rechnen muss. | |||
||[//grundschullernportal.zum.de/images/4/4b/Knobelkartei-A46.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A47.png|miniatur]]||Zwischen der Gondel von Mia und Momo liegen auf einem Halbkreis 6 weitere Gondeln (4, 5, 6, 7, 8 und 9). Also müssen müssen auch auf dem zweiten Halbkreis 6 weitere Gondeln sein. Zwei dieser Gondeln müssen die Nummer 1 und 2 tragen. Folglich bleiben vier Gondeln, die die Nummern 11, 12, 13 und 14 tragen. Hilfreich ist bei der Lösung dieser Aufgabe eine Zeichnung. | |||
||[//grundschullernportal.zum.de/images/2/24/Knobelkartei-A47.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A48.png|miniatur]]||Die folgende Figur besteht aus 7 · 7 = 49 Fliesen, wobei es 3 · 3 = 9 Lücken geben wird. Folglich braucht Mia für die 3. Figur 40 Fliesen.||[//grundschullernportal.zum.de/images/2/2d/Knobelkartei-A48.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A49.png|miniatur]]||Für 8 Brötchen muss Mia 8 · 0,36€ = 2,88€ bezahlen. Sie behält also 2,12€ übrig. Von diesem Geld kann sie 9 Kekse kaufen, für die sei dann 2,07€ bezahlen muss. 5ct behält Mia übrig. | |||
||[//grundschullernportal.zum.de/images/4/45/Knobelkartei-A49.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A50.png|miniatur]]||Folgende Palindromzahlen liegen zwischen 191 und 323: 202, 212, 222, 232, 242, 252, 262, 272, 282, 292, 303, 313. Es sind 12 Zahlen.||[//grundschullernportal.zum.de/images/1/11/Knobelkartei-A50.pdf Download] | |||
|} | |||
===Aufgabe 51-60=== | |||
{| class="wikitable" | |||
|- | |||
!Aufgabe!!Lehrerkommentar!!PDF-Vorlage | |||
|- | |||
|[[Datei:Knobelkartei - A51.png|miniatur]]||Da Mia möglichst wenig tragen möchte, ist sie bestrebt, möglichst viele Kartons mit 12 Eiern zu kaufen. Mit 6 Kartons kann sie auf diese Weise 72 Eier erwerben. Für die beiden fehlenden Eier kann sie entweder einen 6er, aber auch einen 12er Karton kaufen. In jedem Fall braucht sie 7 Kartons. | |||
||[//grundschullernportal.zum.de/images/1/13/Knobelkartei-A51.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A52.png|miniatur]]||Dies ist die erste Knobelaufgabe der Kartei, die nicht zu lösen ist. Mia und Momo haben von Mias Onkel insgesamt 89 Gummibärchen erhalten. Da dies eine ungerade Anzahl ist, ist keine gerechte Verteilung möglich. | |||
||[//grundschullernportal.zum.de/images/9/9e/Knobelkartei-A52.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A53.png|miniatur]]||Die nächste Zahl, bei der alle 5 Ziffern verschieden sind, ist die Zahl 84560. Bis dorthin muss Mias Mutter noch 84560 - 84539 = 21 Kilometer fahren.||[//grundschullernportal.zum.de/images/8/83/Knobelkartei-A53.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A54.png|miniatur]]||Der einfachste Lösungsweg für diese Aufgabe ist natürlich der, bei dem man alle Zahlen von 1 bis 20 aufschreibt und zählt, wie oft die Ziffer 1 vorkommt. Man könnte aber auch den Aufbau des Zahlensystems ausnutzen. Von 0 bis 9 und von 10 bis 19 kommt die 1 jeweils einmal an der Einerstelle vor. Von 10 bis 19 kommt zu sie zudem zehnmal an der Zehnerstelle vor. Somit muss Mia 12 Exemplare der Ziffer 1 kaufen. | |||
||[//grundschullernportal.zum.de/images/b/bc/Knobelkartei-A54.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A55.png|miniatur]]||Der erste Kurs findet am 10. Mai statt. Folglich sind die weiteren Termine im Mai am 17., 24. und 31. Mai. Zwei Termine finden dann noch im Juni statt: 7. und 14. Juni. Somit endet der Kurs am 14. Juni. Ob Mia bis dahin schwimmen gelernt hat? | |||
||[//grundschullernportal.zum.de/images/3/31/Knobelkartei-A55.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A56.png|miniatur]]||Gesucht werden müssen Divisionsaufgaben mit dem Dividenden 33, bei denen der Rest 3 bleibt. Dies sind folgende Aufgaben: | |||
33 : 5 = 6 Rest 3 | |||
33 : 6 = 5 Rest 3 | |||
33 : 10 = 3 Rest 3 | |||
33 : 15 = 2 Rest 3 | |||
33 : 30 = 1 Rest 3 | |||
||[//grundschullernportal.zum.de/images/b/b6/Knobelkartei-A56.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A57.png|miniatur]]||Zur Lösung wird es am einfachsten sein, wenn man sie das dritte Muster dazumalt. Das erste Muster hat 5 schwarze Quadrate. Das zweite Muster besteht schon aus 9 Quadraten. Das dritte Muster besteht aus 17 Quadraten.||[//grundschullernportal.zum.de/images/e/ef/Knobelkartei-A57.pdf Download] | |||
|- | |||
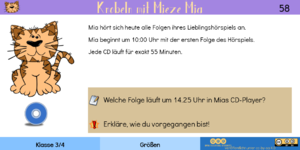
|[[Datei:Knobelkartei - A58.png|miniatur]]||Ein eleganter Lösungsweg ist hier mit Sicherheit das Anlegen einer Tabelle mit den Anfangszeiten der Hörspiele. Anhand der Tabelle ist die richtige Lösung dann schnell abzulesen. | |||
{| class="wikitable" | |||
|Folge | |||
|Startzeit | |||
|- | |||
|1 | |||
|10:00 Uhr | |||
|- | |||
|2 | |||
|10:55 Uhr | |||
|- | |||
|3 | |||
|11:50 Uhr | |||
|- | |||
|4 | |||
|12:45 Uhr | |||
|- | |||
|5 | |||
|13:40 Uhr | |||
|- | |||
|6 | |||
|14:35 Uhr | |||
|} | |||
Somit läuft um 14:25 Uhr noch die fünfte Folge aus Mias Hörspielmarathon. | |||
||[//grundschullernportal.zum.de/images/5/58/Knobelkartei-A58.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A59.png|miniatur]]||Auf den ersten Blick erscheint diese Aufgabe vielleicht besonders schwer. Als (einigermaßen geübter) Mathematiker ist man ggf. geneigt, diese Aufgaben mit zwei Gleichungen zu lösen. Dabei geht es mit ein wenig logischem Denken viel einfacher: | |||
Hätte Mia an jedem der 30 Tage zwei Aufgaben erfunden, hätte sie nun 60 Aufgaben. Sie hat jedoch erst 59 Aufgaben erfunden, so dass sie sich an genau einem Tag nur eine Aufgabe ausgedacht hat. | |||
||[//grundschullernportal.zum.de/images/1/11/Knobelkartei-A59.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A60.png|miniatur]]|| | |||
Bei der Lösung dieser Aufgabe hilft es, wenn man sich die Zahlen der 7er-Reihe aufschreibt und anschließend überlegt, welche darauf folgende Zahl zur 5er-Reihe gehört. Diese Zahlen müssen dann die Altersangaben der drei Frauen sein: | |||
{| class="wikitable" | |||
|7er Reihe | |||
|Alter im nächsten Jahr | |||
|passt? | |||
|- | |||
|7 | |||
|8 | |||
| | |||
|- | |||
|14 | |||
|15 | |||
|ja | |||
|- | |||
|21 | |||
|22 | |||
| | |||
|- | |||
|28 | |||
|29 | |||
| | |||
|- | |||
|35 | |||
|36 | |||
| | |||
|- | |||
|42 | |||
|43 | |||
| | |||
|- | |||
|49 | |||
|50 | |||
|ja | |||
|- | |||
|56 | |||
|57 | |||
| | |||
|- | |||
|63 | |||
|64 | |||
| | |||
|- | |||
|70 | |||
|71 | |||
| | |||
|- | |||
|77 | |||
|78 | |||
| | |||
|- | |||
|84 | |||
|85 | |||
|ja | |||
|} | |||
||[//grundschullernportal.zum.de/images/c/c9/Knobelkartei-A60.pdf Download] | |||
|} | |||
===Aufgabe 61-70=== | |||
{| class="wikitable" | |||
|- | |||
!Aufgabe!!Lehrerkommentar!!PDF-Vorlage | |||
|- | |||
|[[Datei:Knobelkartei - A61.png|miniatur]]||Die Lösung der Aufgabe springt den Schüler*innen vermutlich nicht direkt ins Auge, weil 50 Minuten kein Vielfaches von 20 Minuten ist. Man kann also die Fahrleistung der beiden Katzen nicht auf direktem Wege vergleichen. Dafür muss man erst ermitteln, welche Distanz Mia in 10 Minuten schafft. Dies sind 3 Kilometer. Folglich wird Mia in 50 Minuten 5 · 3km = 15km zurücklegen. Damit ist Mia ein bisschen schneller also Momo. Profis möchten vielleicht sogar die genaue Geschwindigkeit ausrechnen: Mia fährt in einer Stunde 6 · 3km =18km, schafft also 18 km/h. Momo fährt in 10 Minuten 2,8km, schafft also in einer Stunde 16,8km, was einer Geschwindigkeit von 16,8km/h entspricht. | |||
||[//grundschullernportal.zum.de/images/d/df/Knobelkartei-A61.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A62.png|miniatur]]||Vorab die richtige Lösung: Mias Onkel Manuel ist 45 Jahre alt, denn 45 + 4 + 5 = 54. Die Kinder werden dies am ehesten durch ausprobieren herausbekommen. Die mathematische Herleitung ist ein wenig komplexer: | |||
Aus den Bedingungen der Aufgabe ergibt sich folgende Gleichung: 10a + b + a + b = 10b + a | |||
Diesen Term kann man Umwandeln, auflösen und zusammenfassen zu 5a = 4b, wobei für a und b nur ganzzahlige Werte in Frage kommen. Dies passt nur, wenn a=4 und b=5 sind, wodurch sich dann die Zahlen 45 und 54 ergeben. Kinder werden diesen Weg mit Sicherheit nicht gehen :) | |||
||[//grundschullernportal.zum.de/images/c/cc/Knobelkartei-A62.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A63.png|miniatur]]||Diese Aufgabe hat eine gewisse Ähnlichkeit zu dem 3-Krüge-Problem. Zuerst muss Mia beide Uhren umdrehen. Wenn die 3-Minuten-Uhr abgelaufen ist, dreht Mia diese erneut um. In der 5-Minuten-Uhr sind jetzt noch 2 Restminuten übrig. Wenn diese Restminuten abgelaufen sind, dreht sie 5-Minuten-Uhr erneut um. In der 3-Minuten-Uhr laufen nun noch 60 Sekunden ab. Wenn diese verstrichen sind, sind in der 5-Minuten-Uhr noch 4-Minuten Restsand. Somit kann Mia dann exakt 4 Minuten abmessen. | |||
||[//grundschullernportal.zum.de/images/7/7d/Knobelkartei-A63.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A64.png|miniatur]]|| | |||
Hier dürfte eine Tabelle bei der Lösung hilfreich sein: | |||
{| class="wikitable" | |||
|Tag | |||
|Taschengeld heute | |||
|Summe bisher | |||
|- | |||
|1 | |||
|1 Cent | |||
|0,01 € | |||
|- | |||
|2 | |||
|2 Cent | |||
|0,03 € | |||
|- | |||
|3 | |||
|4 Cent | |||
|0,07 € | |||
|- | |||
|4 | |||
|8 Cent | |||
|0,15 € | |||
|- | |||
|5 | |||
|16 Cent | |||
|0,31 € | |||
|- | |||
|6 | |||
|32 Cent | |||
|0,63 € | |||
|- | |||
|7 | |||
|64 Cent | |||
|1,27 € | |||
|- | |||
|8 | |||
|128 Cent | |||
|2,57 € | |||
|- | |||
|9 | |||
|256 Cent | |||
|5,11 € | |||
|- | |||
|10 | |||
|512 Cent | |||
|10,23 € | |||
|- | |||
|11 | |||
|1024 Cent | |||
|20,47 € | |||
|- | |||
|12 | |||
|2048 Cent | |||
|40,95 € | |||
|- | |||
|13 | |||
|4096 Cent | |||
|81,91 € | |||
|- | |||
|14 | |||
|8192 Cent | |||
|'''163,83 €''' | |||
|} | |||
||[//grundschullernportal.zum.de/images/9/90/Knobelkartei-A64.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A65.png|miniatur]]||Der schnellste Weg zur Lösung dieser Aufgabe ist das systematische Ausprobieren. In diesem Fall legt man dafür die Länge einer Fahnenseite fest und sieht sich an, welchen Wert dann die andere Seite annehmen müsste. | |||
Nehmen wir an, die erste Seite wäre nur eine Meter lang. Die zweite Seite nennen wir b. Dann wäre (1 + 1 + b + b) · 9,50 + 1 · b · 7 = 137. b wäre dann 4,538 .... als auf jeden Fall kein ganzzahliger Wert. | |||
Nehmen wir an, die erste Seite wäre nun zwei Meter lang. Die zweite Seite nennen wir b. Dann wäre (2 + 2 + b + b) · 9,50 + 2 · b · 7 = 137. b wäre dann 3. Somit ist eine ganzzahlige Lösung gefunden. | |||
||[//grundschullernportal.zum.de/images/3/3b/Knobelkartei-A65.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A66.png|miniatur]]||Intuitiv denkt man wohl schnell, dass die größte Summe um 23:59:59 erreicht wird. Die größte Ziffernsumme der Sekunden und Minuten erreicht man mit der Zahl 59 (5 + 9 = 14). Die größte Summer bei den Stunden erreicht man jedoch nicht um 23 Uhr (2 + 3 = 5). Um 19 Uhr jedoch ist die Summe der Stundenziffern 10. Somit kann eine Gesamtsumme von 38 erreicht werden. | |||
||[//grundschullernportal.zum.de/images/8/88/Knobelkartei-A66.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A67.png|miniatur]]||Das Gebäude ist insgesamt 7 Würfelchen breit, 3 Würfel hoch und 3 Würfel tief. Die Maße das Paketes müssen als insgesamt 63 cm (Breite), 27 cm (Höhe) und 27 cm Tiefe sein. | |||
||[//grundschullernportal.zum.de/images/9/93/Knobelkartei-A67.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A68.png|miniatur]]||Diese Aufgabe schließt direkt an die Aufgabe Nr. 67 an. Hier muss das Würfelgebäude nun mental zerlegt werden, um die Gesamtzahl der Würfel zu bestimmen, da nicht alle Würfel aus dieser Perspektive sichtbar sind. | |||
In der obersten Schicht liegen 3 + 3 = 6 Würfel. In der mittleren Schicht sind es 7 + 3 = 10 Würfel. In der untersten Schicht sind es 7 + 5 + 3 = 15 Würfel. Insgesamt sind es also 31 Würfel. | |||
Da ein Würfel 18g wiegt, wiegt das gesamte Würfelgebäude 18g · 31 = 558g. Inklusive des Kartons wiegt das gesamte Paket also 688g. | |||
||[//grundschullernportal.zum.de/images/e/e8/Knobelkartei-A68.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A69.png|miniatur]]||In Mias Klasse sind insgesamt 29 Kinder. 3 Kinder haben kein Haustier, also haben 29 - 3 = 26 Kinder wenigstens einen Hamster oder ein Meerschweinchen. 14 Kinder haben einen Hamster. Daher haben 26 - 14 = 12 Kinder auf jeden Fall ein Meerschweinchen, denn sonst hätten ja noch mehr Kinder kein Haustier. Insgesamt gibt es 19 Kinder mit Meerschweinchen. Daher müssen 19 - 12 = 7 Kinder, die schon einen Hamster haben, wohl auch ein Meerschweinchen haben. | |||
||[//grundschullernportal.zum.de/images/7/71/Knobelkartei-A69.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A70.png|miniatur]]||Wenn Manuel bei der ersten Fahrt unbedingt vorne sitzen möchte, kann er entweder, mit Mia, Momo oder Marcel fahren. Das wären drei Kombinationen. Allerdings ist natürlich nicht gesagt, dass Manuel auch die erste Fahrt machen muss. Es könnten auch Mia/Marcel (oder Marcel/Mia), Mia/Momo (oder Momo/Mia) oder Marcel/Momo (oder Momo/Marcel fahren). Das wären 6 weitere Kombinationen, so dass insgesamt 9 Varianten in Fragen kommen. | |||
||[//grundschullernportal.zum.de/images/c/c4/Knobelkartei-A70.pdf Download] | |||
|} | |||
===Aufgabe 71-80=== | |||
{| class="wikitable" | |||
|- | |||
!Aufgabe!!Lehrerkommentar!!PDF-Vorlage | |||
|- | |||
|[[Datei:Knobelkartei - A71.png|miniatur]]||Wenn die 4 Kinder zusammen 12 Sammelkarten haben und Mia 4 Karten besitzt, dann haben Marcel, Manuela und Momo zusammen 8 Karten. Gesucht wird also eine additive Zerlegung der Zahl 8 mit 3 Summanden, wobei sich die 3 Summanden voneinander unterscheiden müssen und kein Summand 0 ist. | |||
Die einzige infrage kommenden Zerlegungen ist 5 + 1 + 2 = 8. Da Momo die meisten Karten besitzt, muss er also 5 Karten haben. | |||
||[//grundschullernportal.zum.de/images/3/38/Knobelkartei-A71.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A72.png|miniatur]]||Diese Aufgabe ist (ausnahmsweise einmal) recht simpel zu lösen. Mia hatte 20 - 17 = 3 Fehlwürfe. Da Momo dreimal so oft verfehlt hat, sind es bei ihm 9 Fehlwürfe und ebenso 17 Treffer. Er hat also 26 Wasserbomben geworfen. | |||
||[//grundschullernportal.zum.de/images/2/24/Knobelkartei-A72.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A73.png|miniatur]]||Mia beginnt bei der Fütterung mit den Kaninchen. Für die 3 Tiere gibt es 3 · 2 · 1 = 6 Möglichkeiten, diese in einer Reihenfolge zu bringen. Anschließend sind die Meerschweinchen dran. Für diese gibt es zwei Möglichkeiten. Nun kann Mia nach jeder "Kaninchen-Reihenfolge" noch zwischen den beiden "Meerschweinchen-Reihenfolgen" wählen, so dass es insgesamt 6 · 2 = 12 Varianten gibt. | |||
||[//grundschullernportal.zum.de/images/4/40/Knobelkartei-A73.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A74.png|miniatur]]||Wenn Mia der Kassiererin einen 20€-Schein überreicht und 1€ zurückbekommt, dann hat ihr Einkauf wohl 19€ gekostet. Hätte Mia nur Dahlien und Hortensien gekauft, dann wäre der Wert ihres Einkaufs immer eine gerade Zahl. Somit muss Mia mindestens eine Geranie gekauft haben. | |||
||[//grundschullernportal.zum.de/images/7/70/Knobelkartei-A74.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A75.png|miniatur]]||Bei der Lösung der Aufgabe muss beachtet werden, dass hier nicht die Anzahl der zu tragenden Gegenstände wichtig ist, sondern deren Gewicht. Alle Zutaten zusammen wiegen 950g, so dass für die beiden Katzen je 475g zu tragen wären. Auch wenn nicht explizit danach gefragt ist, gibt es natürlich verschiedene Möglichkeiten ... doch dazu gibt es dann morgen eine Aufgabe. | |||
||[//grundschullernportal.zum.de/images/2/2c/Knobelkartei-A75.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A76.png|miniatur]]|| | |||
Es gibt zwei Möglichkeiten, wie Mia und Momo die Einkäufe gerecht nach Hause tragen können: | |||
{| class="wikitable" | |||
|Nr. | |||
|Mia | |||
|Momo | |||
|- | |||
|1 | |||
|Eisbergsalat | |||
Fleischtomate | |||
Gurke | |||
|Paprika | |||
Zucchini | |||
Gurke | |||
|- | |||
|2 | |||
|Paprika | |||
Zucchini | |||
Gurke | |||
|Eisbergsalat | |||
Fleischtomate | |||
Gurke | |||
|} | |||
||[//grundschullernportal.zum.de/images/6/66/Knobelkartei-A76.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A77.png|miniatur]]||Wenn Mias Mutter dreimal so viele Erdbeeren wie Mias Mutter hat, dann haben beide zusammen vier Anteile Erdbeeren: Mia hat einen Anteil und die Mutter drei Anteile. Wenn man also das Gesamtgewicht durch 4 dividiert, erhält man das Gewicht von Mias Anteil. 1832 : 4 = 458g | |||
Mia hat also 458g Erdbeeren gepflückt (bzw. ist ihr Korb so schwer). | |||
||[//grundschullernportal.zum.de/images/2/2c/Knobelkartei-A77.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A78.png|miniatur]]||Bei dieser Aufgabe müssen die beiden Schrägansichtern der Wasserbombentürme mental zerlegt werden, um die jeweilige Gesamtzahl der gestapelten Wasserballons zu ermitteln. Schließlich müssen diese dann noch verglichen werden. | |||
Momo: Momos Stapel besteht in der untersten Schicht aus einem 3x3-Quadrat, in der mittleren Schicht aus einem 2x2-Quadrat und oben aus einem einzelnen Ballon. Es sind also 9 + 4 + 1 = 14 Ballons. | |||
Mia: Mias Stapel besteht aus Dreicken. das unterste Dreieck besteht aus 4+3+2+1=10 Ballons. Das zweite Dreieck aus 3+2+1=6 Ballons. Das dritte Dreieck aus 2+1=3 Ballons und zuoberst liegt ein weiterer Ballon. Es sind also 10 + 6 + 3 + 1 = 20 Ballons. Mia hat also 6 Wasserbomben mehr! | |||
||[//grundschullernportal.zum.de/images/6/6c/Knobelkartei-A78.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A79.png|miniatur]]||Die Kurzfassung der Lösung ist: in die Momos Schachtel passen 6-mal so viele Kirschen hinein. Diese Einsicht erreicht am ehesten, wenn man konkrete Zahlen für Mias Schachtel annimmt. Legt man beispielsweise fest, dass die Schachtel 10cm hoch, 10cm breit und 10cm tief ist, so hat sie ein Volumen von 10cm · 10cm · 10cm = 1000 cm³. Momos Schachtel ist dann jedoch 30cm · 20cm · 10cm = 6000cm³ groß, also 6-mal so groß. | |||
||[//grundschullernportal.zum.de/images/9/9e/Knobelkartei-A79.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A80.png|miniatur]]|| | |||
Der sicherste Weg zur Lösung dieser Aufgabe ist eine Rechentabelle, auch wenn dieser Weg natürlich recht langwierig ist. Man kann zu der Aufgabe diese Tabelle anlegen: | |||
{| class="wikitable" | |||
|Schafe | |||
|Köpfe | |||
|Beine | |||
|Differenz | |||
|- | |||
|1 | |||
|1 | |||
|4 | |||
|3 | |||
|- | |||
|2 | |||
|2 | |||
|8 | |||
|6 | |||
|- | |||
|3 | |||
|3 | |||
|12 | |||
|9 | |||
|- | |||
|4 | |||
|4 | |||
|16 | |||
|12 | |||
|- | |||
|5 | |||
|5 | |||
|20 | |||
|15 | |||
|- | |||
|6 | |||
|6 | |||
|24 | |||
|18 | |||
|- | |||
|7 | |||
|7 | |||
|28 | |||
|21 | |||
|} | |||
Natürlich kann man auch einen direkteren Weg zur Lösung gehen: Jedes Schaf hat 1 Kopf und 4 Beine. Die Differenz zwischen der Anzahl der Köpfe und Beine ist also immer 3. Die Differenz auf der Weide nun 21 ist, müssen wohl 21 : 3 = 7 Schafe auf der Weide stehen. | |||
||[//grundschullernportal.zum.de/images/e/eb/Knobelkartei-A80.pdf Download] | |||
|} | |||
===Aufgabe 81-90=== | |||
{| class="wikitable" | |||
|- | |||
!Aufgabe!!Lehrerkommentar!!PDF-Vorlage | |||
|- | |||
|[[Datei:Knobelkartei - A81.png|miniatur]]||Mia legt mir ihren Erbsen Dreiecks- und Quadratzahlen. Die Reihe der Quadratzahlen lautet 1, 2, 4, 9, 16, 25, 36, 49, ... . Die Reihe der Dreieckszahlen lautet 1, 3, 6, 10, 15, 21, 28, 36, 45, ... | |||
Mia wird also bei der 6. Quadratzahl und der 8. Dreieckszahl merken, dass ihre Formen aus der gleichen Anzahl Erbsen bestehen. | |||
||[//grundschullernportal.zum.de/images/d/d3/Knobelkartei-A81.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A82.png|miniatur]]||Wenn Mia auf dem ersten Foto 5 Beine fotografiert hat, dann sind im Gehege höchstens 5 Flamingos, denn 6 Flamingos würden auf mindestens 6 Beinen stehen müssen (es sei denn, ein Flamingo fliegt gerade weg). | |||
Da Mia auf einem Foto aber 9 Beine sieht, müssen aus auch mindestens 5 Flamingos sein. 4 Flamingos haben zusammen höchstens 8 "ausgeklappte" Beine. Somit ist klar, dass im Gehege 5 Flamingos stehen. | |||
||[//grundschullernportal.zum.de/images/1/11/Knobelkartei-A82.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A83.png|miniatur]]||Für Kombinatorik-Profis ist diese Aufgabe recht einfach: Für Hamster 1 gibt es 4 Möglichkeiten der Namensgebung. Nachdem man diesen Namen festgelegt hat, gibt es für Hamster 2 noch 3 Möglichkeiten (da ein Name nun vergeben ist). Für den Hamster 3 gibt es dann nur noch zwei Varianten, während der letzte Hamster immer den Namen bekommt, der übrig bleibt. Dadurch gibt es 4 · 3 · 2 · 1 = 24 Möglichkeiten, wie Mia die Hamster benennen kann. | |||
Die Schüler*innen könnten sich als Unterstützung 4 Hamster aufmalen oder mit Spielfiguren darstellen und Namensschildchen verschieben, um alle Varianten zu finden. | |||
||[//grundschullernportal.zum.de/images/8/84/Knobelkartei-A83.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A84.png|miniatur]]||Bei dieser Aufgabe handelt es sich eigentlich schon fast um eine klassische Sachaufgabe, die aber durch die Vielzahl an Informationen und die verschiedenartigen Rechenschritte besonders schwierig wird. Was muss im Einzelnen getan werden? | |||
Das Volumen des Pools muss berechnet werden: 3m · 2m · 1m = 6m³ = 300cm · 200cm · 100cm = 6.000.000 cm³ = 6000 Liter | |||
Die Füllzeit muss berechnet werden: 6000 Liter : 20 Liter/Minuten = 300 Minuten = 5 Stunden | |||
Die Ende der Füllzeit muss berechnet werden: 12.00 Uhr + 5 Stunden = 17.00 Uhr | |||
||[//grundschullernportal.zum.de/images/a/a7/Knobelkartei-A84.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A85.png|miniatur]]||Mia kommt erst um 17.10 Uhr zum Training. Sie knickt zwar um 17.55 Uhr am, ihr Training wäre aber eigentlich erst um 17.55 Uhr + 10 Minuten = 18.05 Uhr zu Ende gewesen. Seit 17.10 Uhr sind bis dahin 55 Minuten vergangen. | |||
Da Mia aber erst zur Mitte des Trainings gekommen ist (um 17.10 Uhr), hat das Training also 55 Minuten früher begonnen. 17.10 Uhr - 55 Minuten = 16.15 Uhr. Ihr Training hätte also um 16.15 Uhr begonnen! | |||
||[//grundschullernportal.zum.de/images/9/9c/Knobelkartei-A85.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A86.png|miniatur]]||Wenn der Monatserste ein Donnerstag ist, dann ist der 28. des Monats ein Mittwoch. Bis dahin sind vier viele Wochen vergangen, die jeweils 5 Schultage haben. Es sind also 20 Schultage gewesen. Der 29. wäre wieder ein Donnerstag und somit der 21. Schultag. Der 30. wäre ein Freitag und der 22. Schultag. Ganz gleich ob wir nun einen Monat mit 30 oder 31 Tagen haben ... der 31. wäre auf jeden Fall ein Samstag und damit schulfrei. Mia kauft sich also 22 Brötchen, wobei Brötchen 6, 12 und 18 kostenfrei sind. Also muss sie nur 19 Brötchen bezahlen. | |||
||[//grundschullernportal.zum.de/images/3/39/Knobelkartei-A86.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A87.png|miniatur]]||Wenn Mia an 60 Tagen je eine Aufgabe gelöst hat und an 25 Tagen sogar ja zwei Aufgaben geschafft hat, dann hat sie an zusammen 85 Tagen schon 110 Aufgaben geschafft. Es bleiben also 140 - 110 = 30 Aufgaben übrig, die sie immer in Dreierbündeln gelöst hat. Dafür wird sie dann 10 Tage benötigt haben. Sie hat also bisher an 85 + 10 = 95 Tagen geknobelt. | |||
||[//grundschullernportal.zum.de/images/d/d4/Knobelkartei-A87.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A88.png|miniatur]]||Aus rein mathematischer Sicht lässt sich diese Aufgabe wieder mit zwei Gleichungen und zwei Unbekannten lösen (Zweierzimmer = x; Dreierzimmer =y): | |||
x + y = 32; 2x + 3y = 81 | |||
=> x = 32 - y; 2(32 - y) + 3y = 81 | |||
=> x = 32 - y; 64 - 2y + 3y =81 | |||
=> x = 32 - y; y = 17 | |||
=> x = 32 - 17 = 15 | |||
Es gibt also 15 Doppel- und 17 Dreierzimmer. | |||
Schüler kommen wohl mit systhematischem Probiern am besten voran. Man legt eine Zahl für die Doppelzimmer fest und schaut dann, wie viele Dreierzimmer sich dann ergeben. | |||
||[//grundschullernportal.zum.de/images/8/8a/Knobelkartei-A88.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A89.png|miniatur]]||Um eine sinnvolle Lösung zu entwickeln, sollte man zuerst überlegen, wie viel Flüssigkeit in allen 15 Flaschen insgesamt vorhanden ist. Dies sind 5 · 100ml + 5 · 400ml + 5 · 700ml = 6000ml. Folglich muss jede Katze 5 Flaschen mit insgesamt 2000ml Flüssigkeit bekommen. | |||
Folgende Aufteilungen sind möglich: | |||
700ml + 700ml + 400ml + 100ml + 100ml = 2000ml | |||
700ml + 700ml + 400ml + 100ml + 100ml = 2000ml | |||
700ml + 100ml + 400ml + 400ml + 400ml = 2000ml | |||
||[//grundschullernportal.zum.de/images/a/a9/Knobelkartei-A89.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A90.png|miniatur]]||Diese Sachaufgabe muss in mehreren Schritten gelöst werden. Zuerst muss ermittelt werden, wie viele Tonpapierbögen Mia braucht. Aus einem Bogen kann Mia (wenn sie geschickt ist), 10 Einladungen schneiden (70cm : 14cm = 5; 50cm : 25cm = 2; 2 · 5 = 10). | |||
Mia muss also 4 Bögen kaufen, um 34 Einladungen basteln zu können. 4 Bogen kosten 4 · 0,75€ = 3,00€ | |||
Mia muss also 3,00€ ausgeben. | |||
||[//grundschullernportal.zum.de/images/3/37/Knobelkartei-A90.pdf Download] | |||
|} | |||
===Aufgabe 91-100=== | |||
{| class="wikitable" | |||
|- | |||
!Aufgabe!!Lehrerkommentar!!PDF-Vorlage | |||
|- | |||
|[[Datei:Knobelkartei - A91.png|miniatur]]|| | |||
Hier wird eine Zahl gesucht, die sowohl ein Vielfaches von 8, als auch ein Vielfaches von 6 ist, bei Division durch 7 aber einen Rest von 5 lässt. Diese findet man unter anderem, wenn man sich folgende Tabelle erstellt: | |||
{| class="wikitable" | |||
|8er-Reihe | |||
|Vielfaches von 6? | |||
|Rest bei Division durch 7 | |||
|- | |||
|8 | |||
|nein | |||
| --- | |||
|- | |||
|16 | |||
|nein | |||
| --- | |||
|- | |||
|24 | |||
|ja | |||
|3 | |||
|- | |||
|32 | |||
|nein | |||
| --- | |||
|- | |||
|40 | |||
|nein | |||
| --- | |||
|- | |||
|48 | |||
|ja | |||
|6 | |||
|- | |||
|56 | |||
|nein | |||
| --- | |||
|- | |||
|64 | |||
|nein | |||
| --- | |||
|- | |||
|72 | |||
|ja | |||
|2 | |||
|- | |||
|80 | |||
|nein | |||
| --- | |||
|- | |||
|88 | |||
|nein | |||
| --- | |||
|- | |||
|96 | |||
|ja | |||
|5 | |||
|} | |||
Folglich ist 96 die kleinste Zahl, die alle drei Bedingungen erfüllt. | |||
||[//grundschullernportal.zum.de/images/c/c4/Knobelkartei-A91.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A92.png|miniatur]]|| | |||
Die Kinder werden bei dieser Aufgabe (wenn sie sie gelöst haben) von dem rasanten Wachstum erstaunt sein. Der Text wird ggf. nicht sofort verstanden. Jede Katze erzählt abends 3 neuen Katzen von dem See. Am Tag darauf gehen alle Katzen zum See: Die, die bereits am Vortag da waren und die, die neu von dem See erfahren haben. | |||
Auch hier hilft eine Tabelle: | |||
{| class="wikitable" | |||
|Tag | |||
|Katzen zum See | |||
|Sie erzählen es ___ Katzen | |||
|- | |||
|Montag | |||
|1 | |||
|3 | |||
|- | |||
|Dienstag | |||
|4 | |||
|12 | |||
|- | |||
|Mittwoch | |||
|16 | |||
|48 | |||
|- | |||
|Donnerstag | |||
|64 | |||
|192 | |||
|- | |||
|Freitag | |||
|256 | |||
|768 | |||
|- | |||
|Samstag | |||
|1024 | |||
|3072 | |||
|- | |||
|Sonntag | |||
|4096 | |||
| --- | |||
|} | |||
Am Sonntag kommen also 4096 Katzen zum See ... hätte Mia mal lieber den Mund gehalten ;). | |||
||[//grundschullernportal.zum.de/images/f/f3/Knobelkartei-A92.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A93.png|miniatur]]||Die Pyramide, die Mia bauen will, besteht aus den ersten 5 Dreieckszahlen (1, 3, 6, 10, 15), also aus 1 + 3 + 6 + 10 + 15 = 35 Ballons. | |||
Mia hat (wie man bereits sieht) 19 Ballons gestapelt, so dass noch 35 - 19 = 16 Ballons fehlen. | |||
||[//grundschullernportal.zum.de/images/d/d8/Knobelkartei-A93.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A94.png|miniatur]]||Bei dieser Aufgabe ist die Begründung von besonderer Bedeutung, denn ein "ja" oder ein "nein" ist als Antwort ja auch mal schnell geraten. Um zu ermitteln, ob das Papier für das Geschenk passt, kann zum Beispiel über eine Abwicklung des Kartons in ein Netz geschehen. In der Grafik ist ein solches Netz dargestellt. Die Außenmaße dieses Netztes übersteigen sowohl die Breite, als auch die Länge des Geschenkpapiers. | |||
Nun könnte man natürlich noch anbringen, dass es ja mehrer mögliche Netze zum diesem Körper gibt. Diese alle zu untersuchen dauert in der Tat recht lange. Um die letzten Zweifel auszuräumen, kann man sich also den Flächeninhalt der 6 Seitenflächen ansehen. Diese sind: | |||
20cm · 10cm = 200cm² (taucht zweimal auf) | |||
20cm · 15cm = 300cm² (taucht zweimal auf) | |||
10cm · 15cm = 150cm² (taucht zweimal auf) | |||
Der gesamte Flächeninhalt beträgt also 1300cm². Das Stück Geschenkpapier kommt jedoch insgesamt nur auf 1200cm². Es wird also keinesfalls passen. | |||
||[//grundschullernportal.zum.de/images/9/93/Knobelkartei-A94.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A95.png|miniatur]]||Diese Aufgabe lässt sich natürlich mit (7) Kindern nachspielen. Die erste Spielerin muss 6 Mitspielerinnen umarmen. Für die zweite Spielerin bleiben dann noch 5 Mitspielerinnen übrigen, denn mit der ersten Spielerin gab es ja bereits eine Umarmung. Dies lässt sich munter fortführen. Die siebte und letzte Spielerin wurde dann bereits von allen Mitspielerinnen umarmt. Somit gibt es 6 + 5 + 4 + 3 + 2 + 1 + 0 = 21 Umarmungen nach dem Spiel. | |||
||[//grundschullernportal.zum.de/images/4/42/Knobelkartei-A95.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A96.png|miniatur]]|| | |||
Diese Aufgabe gibt es in unzähligen Variationen. Mit einer Tabelle lässt sich am besten deutlich machen, welches die korrekte Lösung ist: | |||
{| class="wikitable" | |||
|Tag | |||
|Start | |||
|Ende | |||
|- | |||
|1 | |||
|0 | |||
|0,5m | |||
|- | |||
|2 | |||
|0,25m | |||
|0,75m | |||
|- | |||
|3 | |||
|0,5m | |||
|1,0m | |||
|- | |||
|4 | |||
|0,75m | |||
|1,25m | |||
|- | |||
|5 | |||
|1,0m | |||
|1,5m | |||
|- | |||
|6 | |||
|1,25m | |||
|1,75m | |||
|- | |||
|7 | |||
|2,0m | |||
|2,5m | |||
|- | |||
|8 | |||
|2,25m | |||
|2,75m | |||
|- | |||
|9 | |||
|2,5m | |||
|3,0m | |||
|- | |||
|10 | |||
|2,75m | |||
|3,25m | |||
|- | |||
|11 | |||
|3,0m | |||
|3,5m | |||
|- | |||
|12 | |||
|3,25m | |||
|3,75m | |||
|- | |||
|13 | |||
|3,5m | |||
|4,0m | |||
|} | |||
Am Abend des 13. Tages ist Mia also bei 4 Metern angekommen. | |||
||[//grundschullernportal.zum.de/images/f/f0/Knobelkartei-A96.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A97.png|miniatur]]||Den Kindern wird bei der Lösung der Aufgabe hoffentlich schnell klar sein, dass die beiden Katzen zusammen weniger als eine Stunde brauchen werden. Dann werden sie ggf. versuchen zu ermitteln, wie viel Garten die Katzen z.B. in einer halben Stunde schaffen und dann ggf. schrittweise die Arbeitszeit erhöhen. Es gibt jedoch ein viel einfacheren Weg, für den man aber ein wenig um die Ecke denken muss: | |||
Mia schafft in 2 Stunden einen Garten. Momo würde in dieser Zeit 2 Gärten schaffen. Zusammen schaffen die Katzen also in 120 Minuten 3 Gärten. Für einen Garten brauchen sie dann also 120min : 3 = 40min. Gemeinsam können sie die Arbeit also in 40 Minuten erledigen. | |||
||[//grundschullernportal.zum.de/images/f/f3/Knobelkartei-A97.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A98.png|miniatur]]||Wenn Mia inzwischen bei Seite 96 angelangt ist, dann hat sie 96 : 6 = 16 "Päckchen" á 9 Minuten gelesen, also ingesamt 144 Minuten gelesen. Momo schafft in dieser Zeit 144 : 6 = 24 Päckchen á 6 Minuten. In jedem Zeitraum von 6 Minuten liest er 5 Seiten, also er nun schon 24 · 5 = 120 Seiten gelesen. | |||
||[//grundschullernportal.zum.de/images/5/55/Knobelkartei-A98.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A99.png|miniatur]]||Auch bei dieser Aufgabe muss man ein wenig um die Ecke denken, damit man sich nicht in komplizierten Rechnungen verzettelt. Es lohnt sich zu überlegen, was der Unterschied zwischen Einkaufsmöglichkeit 1 und 2 ist. Für 3 Schokoriegel und 2 Bonbons weniger bekommt Mia 3 Sticker mehr. Lässt Mia also bei der zweiten Variante wiederum 3 Riegel und 2 Bonbons weg, würde sie dafür ebenfalls 3 Sticker mehr bekommen. Dann hätte sie 13 Sticker, dafür aber keine Bonbons und Riegel. | |||
||[//grundschullernportal.zum.de/images/f/f1/Knobelkartei-A99.pdf Download] | |||
|- | |||
|[[Datei:Knobelkartei - A100.png|miniatur]]||Der Satz, den Mia aufschreiben möchte, hat 22 Buchstaben. Folglich kann Mia ihn 45-mal aufschreiben und schafft damit schon 990 aufgeschriebene Buchstaben. Bis zur 1000 sind es dann noch 10 Buchstaben. Der 10. Buchstabe des Satzes ist das n. Somit schreibt Mia als 1000. Buchstaben das "n" auf. | |||
||[//grundschullernportal.zum.de/images/a/a7/Knobelkartei-A100.pdf Download] | |||
|} | |||
{{DownloadBox | |||
|Titel = Alle Aufgaben in einer Datei | |||
|PDF = Knobelkartei - Gesamt 3er.pdf | |||
|Beschreibung = je 3 Kopien pro Seite | |||
}} | |||
{{DownloadBox | |||
|Titel = Alle Aufgaben in einer Datei | |||
|PDF = Knobelkartei - Gesamt.pdf | |||
|Beschreibung = je 3 verschiedene Aufgaben pro Seite | |||
}} | |||
==Material== | ==Material== | ||
{{DownloadBox | |||
|Titel = Etiketten Knobelkartei 3/4 | |||
|PDF = KnobelkarteiZ-ZEtiketten.pdf | |||
|Beschreibung = je 8 verschiedene Etiketten pro Seite | |||
}} | |||
Etiketten | {{DownloadBox | ||
|Titel = Etiketten Knobelkartei 3/4 | |||
Etiketten | |PDF = KnobelkarteiZ-ZEtikettenZ8er.pdf | ||
|Beschreibung = je 8 gleiche Etiketten pro Seite | |||
}} | |||
{{DownloadBox | |||
|Titel = Arbeitsheft Knobelkartei | |||
|PDF = Mia-Knobelaufgaben.1.pdf | |||
|Beschreibung = Arbeitsheft zum Einkleben der Kartei-Etiketten | |||
}} | |||
[[Kategorie:Lehrerportal]] [[Kategorie:Mathematik]] | [[Kategorie:Lehrerportal]] | ||
[[Kategorie:Mathematik]] | |||
Aktuelle Version vom 3. November 2019, 08:48 Uhr
"Knobeln mit Mieze Mia" ist eine gemeinschaftliche entwickelte Knobelkartei unter offener Nutzungslizenz.
Gemeinschaftlich entwickelt
Zur Knobelkartei werden alle Quelldateien mitveröffentlich. Daher sind alle interessierten Nutzer aufgerufen, an der Weiterentwicklung der Kartei mitzuwirken. Vorschläge für neue Aufgaben können auf dieser Seite eingereicht werden. Dabei spielt es keine Rolle, ob die Aufgaben schon die Vorlage eingefügt sind oder nur als Text in der Mail umschrieben werden.
Offene Nutzungslizenz
Die Aufgaben und Materialien der Knobelkartei sind unter einer creative-commons-Lizenz veröffentlicht. Dies ermöglicht allen Nutzern folgende Rechte
- Teilen — das Material in jedwedem Format oder Medium vervielfältigen und weiterverbreiten
- Bearbeiten — das Material remixen, verändern und darauf aufbauen und zwar für beliebige Zwecke, sogar kommerziell.
Der Lizenzgeber kann diese Freiheiten nicht widerrufen solange Sie sich an die Lizenzbedingungen halten. Dabei geltende folgende Bedingungen:
- Namensnennung — Sie müssen angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade Sie oder Ihre Nutzung besonders.
- Weitergabe unter gleichen Bedingungen — Wenn Sie das Material remixen, verändern oder anderweitig direkt darauf aufbauen, dürfen Sie Ihre Beiträge nur unter derselben Lizenz wie das Original verbreiten.
Vollständiger Lizenztext unter: https://creativecommons.org/licenses/by-sa/4.0/legalcode.de
Sowohl die PDF-Dateien, als auch die Quelldateien, als auch die Bilddateien dürfen (und sollen) z.B. auf Schulhomepages oder an anderer Stelle veröffentlicht werden.
Überlegungen zum Einsatz im Unterricht
Um die noch immer stetig wachsende Knobelkartei im Unterricht zu nutzen, gibt es verschiedene Möglichkeiten. Hier kommt ein erster Vorschlag:
Bei einer zweiten Variante der Aufgabenkarten sind diese wesentlich kleiner gehalten, so dass sie auf selbstklebende Etiketten in DIN-A7 passen. Hierzu haben ich auch eine PDF-Vorlage erstellt, bei der entweder pro Aufgabe ein Etikett und pro Aufgabe eine ganze Seite Etiketten verwendet wurde. Dazu begleitend gibt es eine Druckvorlage für ein Mia-Heft, in das man die Etiketten passgenau einkleben kann. Auf der Seite gibt es dann zusätzlich ein Feld mit Rechenkästchen, ein Blankofeld und ein Feld für die Antwort und die Erklärung des Lösungswegs.
Die Etiketten kann man (ggf. schon geschnitten) in einem Karteikasten o.ä. bereitstellen. Die Schüler*innen können sich dann (in Freiarbeitsphasen etc.) ein Etikett nehmen und dies in ihr Heftchen einkleben, um dann individuell an der Aufgabe zu arbeiten.
Twitterkanal
tbc.
Aufgaben Klasse 3/4
Aufgabe 1-10
| Aufgabe | Lehrerkommentar | PDF-Vorlage | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Diese kombinatorische Aufgabe ist vergleichsweise einfach zu lösen. Für den ersten Würfel gibt es 6 verschiedene Möglichkeiten zu fallen (1 - 6), für den zweiten Würfel ebenfalls. Demnach gäbe es eigentlich 6 · 6 = 36 Möglichkeiten. Hier greift jedoch die Einschränkung, dass nur verschiedene Würfelergebnisse gezählt werden sollen. Die Ergebnisse "1 und 6", sowie "6 und 1" sind in diesem Sinne identisch und werden als ein Ergebnis gewertet. Somit bleiben 21 verschiedene Möglichkeiten übrig:
1 + 1; 1 + 2; 1 + 3; 1 + 4; 1 + 5; 1 + 6; 2 + 2; 2 + 3; 2 + 4; 2 + 5; 2 + 6; 3 + 3; 3 + 4; 3 + 5; 3 + 6; 4 + 4; 4 + 5; 4 + 6; 5 + 5; 5 + 6; 6 + 6 Die Schülerinnen und Schüler werden am ehesten mit einem strukturierten Vorgehen auf die vollständige Lösung kommen: Erst alle Würfelergebnisse mit 1, dann alle Würfelergebnisse mit 2, ..., am Ende alle doppelten Ergebnisse streichen. In diese Richtung könnten auch mögliche Hilfestellungen gehen. |
Download | |||||||||||||||||||
| Diese geometrische Aufgabe lässt sich auf zwei Weisen lösen: kopfgeometrisch, indem man sich den Faltvorgang vorstellt oder enakitv, indem die Faltvorlagen ausgeschnitten und zusammengefaltet werden.
Falsch ist jedenfalls die Vorlage 3, denn die beide Flächen ganz rechts überdecken sich beim Falten, so dass der entstehende Würfel an einer Seite offen ist. |
Download | |||||||||||||||||||
| Diese Aufgabe gehört im Grunde in die Kategorien Arithmetik und Kombinatorik. Gesucht wird eine vierstellige Zahl. Bei der Beschreibung wurde bewusst auf die Verwendung der Stellenwertbezeichnungen (Einer, Hunderter, ...) verzichtet, da Nummern eines Fahrradschloss in der Regel als Set von Einzelziffern ausgesprochen werden. Bei der Lösung empfiehlt es sich, von der dritten Stellen ausgehend zu überlegen und dann nach und nach zu überlegen, was daraus für die zweite und erste Stelle folgt:
Dritte Stelle 1 -> Zweite Stelle 2 -> Erste Stelle 4 Dritte Stelle 2 -> Zweite Stelle 4 -> Erste Stelle 6 Dritte Stelle 3 -> Zweite Stelle 6 -> Erste Stelle 8 Dritte Stelle 4 -> Zweite Stelle 8 -> Erste Stelle 10 -> nicht möglich An vierter Stelle kann nur eine ungerade Ziffer stehen (1, 3, 5, 7, 9). Da es die Zusatzbedingung gibt, dass eine Ziffer in der Geheimnummer doppelt vorkommen muss, ergeben sich folgende Möglichkeiten:
Es gibt also zwei verschiedene Möglichkeiten, die Mia ausprobieren müsste.
|
Download | |||||||||||||||||||
| Da schon bekannt ist, dass "ZeigeLinks" = 2 ist, kann man über die Berechnung der Einerstelle ("DaumenRunter" · "ZeigeLinks" = 2) ermitteln, dass "DaumenRunter" = 1 sein muss. Als nächstes schaut man sich die Berechnung der Hunderterstelle an ("ZeigeRechts" · "ZeigeLinks" = 2) Da man schon weiß, dass "ZeigeLinks" = 2 ist, muss also "ZeigeRechts" = 6 sein. Wenn man danach zur Zehnerstelle zurückgeht, weiß man auch, dass "DaumenHoch" = 3 ist, denn sonst würde die dazugehörende Rechnung "DaumenHoch" · "ZeigeLinks" = 6 nicht zu lösen sein. Bleibt noch die Rechnung der Tausenderstelle: "Victory" · "Victory" = 11. Von der Rechnung der Hunderterstelle haben wir noch einen Übertrag übrig. Daher muss "Victory" = 5 sein, damit die Rechnung aufgehen kann.
Die vollständig gelöste Rechnung lautet dann: 5631 · 2 = 11262 |
Download | |||||||||||||||||||
| Bei dieser Aufgabe steht vor allem die Frage im Vordergrund, welche Rechnung in welcher Reihenfolge durchgeführt werden - und was am Ende mit den Einzelergebnissen gemacht werden muss. Tipps an die Schüler könnten also vor allem in diese Richtung gehen.
Da Mia 54 Bonbons geschenkt bekommen hat, 7 Bonbons aber selbst essen möchte, bleiben ihr zum Verteilen nur noch 47 Stück. 8 + 7 · 3 + 4 = 33 Bonbons werden an eine fest vorgegebene Zahl von 16 Freunden verteilt. Es bleiben also 14 Bonbons übrig, die sie an "den Rest" verteilt, jeweils 2 Bonbons pro Kind. Somit werden diese 14 Bonbons also an 7 Kinder verteilt. Insgesamt verteilt Mia ihre Bonbons also an 23 Freunde - und sich selbst. |
Download | |||||||||||||||||||
| Für die richtige Lösung dieser Aufgabe ist eine Skizze hilfreich. Daher sind direkt unter der Aufgabe die 4 Wegpunkte des 2,6 km langen Weges dargestellt.
Zuerst lässt sich recht einfach bestimmen, wie weit der Weg von Momo zum Spielplatz ist: Wenn Mia zu Momo geht, legt sie 2,6 km zurück. Geht sie jedoch nur bis zum Spielplatz, dann ist der 2,08 km lang. Also muss der Weg vom Spielplatz zu Momo 2,6 km - 2,08 km = 0,052 km lang sein. Geht nun Momo bis zur Kirche, dann ist sein Weg 700 m lang. Zieht man hiervon nun die Wegstrecke ab, die er erstmal bis zum Spielplatz geht, dann erhält man als Ergebnis die Wegstrecke vom Spielplatz bis zur Kirche. 700 m - 520 m = 180 m. Spielplatz und Kirche liegen also nur 180 m auseinander. |
Download | |||||||||||||||||||
Als Hilfsmittel für die Lösung dieser Aufgabe bietet sich eine Rechentabelle an. Beim Ausfüllen der Tabelle ist jedoch zu beachten, dass der Zuwachs beim Schal nicht in gleichen Schritten erfolgt, sondern Mia jeden Tag ein bisschen mehr schafft, weil sie mehr Übung beim Stricken hat. Dies sprachlich zu erfassen und bei der Rechnung umzusetzen, dürfte für die Kinder die größte Hürde sein. An dieser Stelle könnten also erste Tipps ansetzen (neben dem Hinweis auf die Verwendung einer Rechentabelle).
Da Mias Schal 250 cm lang werden soll, wird sie ihren Schal erst am Freitag fertiggestellt haben. |
Download | |||||||||||||||||||
| Die Lösung der Aufgabe wir etwas einfacher, wenn sich im ersten Schritt überlegt, welche Bälle/Zahlen überhaupt nur für das mittlere Feld in Frage kommen. Die Zahlen 16 und 18 scheiden hierbei aus, da die Summe der verbleibenden 4 Bälle dann ungerade wird. Eine ungerade Summe lässt sich jedoch nicht gleichmäßig auf beide Quadrate verteilen.
Somit ergeben sich folgende Möglichkeiten:
Diese drei Lösungen lassen sich natürlich gespiegelt aufschreiben, wodurch es 6 Lösungen gäbe. Zudem gibt es für jede Lösung noch 4 verschiedene Varianten, die 4 Bälle auf die Felder zu verteilen. Dann wären es sogar 24 verschiedene Möglichkeiten. Hier kann jedoch im Gespräch mit den Schülern besprochen werden, ob diese Varianten jeweils als verschiedene oder identische Lösung gewertet werden sollen. |
Download | |||||||||||||||||||
| Um die Länge der Leine zu ermitteln, muss man zuerst die Einzellängen der Wäschestücke mit den jeweiligen Breiten multiplizieren. Die 4 Bettlaken sind 3,8m breit, die T-Shirts 2,1m. Die 10 Socken sind zusammen 1,20m breit. Somit ergibt sich schonmal eine Gesamtbreite von 7,1 m. Insgesamt sind es 20 Wäschstücke, so dass es 19 Zwischenräume á 10cm gibt, was dann in der Summe 1,90m Zwischenraum ergibt. Die Wäscheleine sollte also mindesten 9m lang sein. | Download | |||||||||||||||||||
| Einen echten Lösungsweg gibt zu dieser Aufgabe nicht, da die Aufgabe idealerweise kopfgeometrisch gelöst wird. Bei mentalen Auseinanderbauen des Quaders wird man feststellen, dass sich in der 2. und 3. Schicht in der Mitte je ein Würfel befindet, der keinen Außenkontakt hat. Diese beiden Würfel werden folglich auch nicht angemalt, wenn Mia den großen Quader von außen bemalt. Folglich hat Momo mit seiner Aussage nicht recht. | Download |
Aufgabe 11-20
| Aufgabe | Lehrerkommentar | PDF-Vorlage | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Die Rechnungen hinter dieser Rechengeschichte sind (mathematisch betrachtet) zwei Gleichungen mit zwei Unbekannten: 2€ + 6 Spiele + 3 Hosen = 35€ und 4€ + 7 Spiele + 2 Hosen = 35€. Man könnte jetzt für "Spiele" und "Hosen" Variablen einsetzen, eine gleichen nach "Hosen" auflösen und dann in die zweite Gleichung einsetzen. Dann erhielte man als Lösung: ein Spiel kostet 3€ und eine Hose kostet 5€.
Die Schülerinnen und Schüler werden vermutlich nicht mit Variablen arbeiten. Hier hilft vermutlich systematisches Ausprobieren: einen Betrag für das Spiel annehmen, mit Hilfe des ersten Satzes ausprobieren, was dann die Hose kosten muss und diese Werte dann an der zweiten Gleichung überprüfen. |
Download | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Um die Fairness dieses Würfelspiels einschätzen zu können, muss man die Wahrscheinlichkeiten der beiden Ereignisse bestimmen und auswerten. Beim Würfeln mit zwei Würfeln gibt es 6 · 6 = 36 Möglichkeiten, wie die Würfel fallen können. Hierbei sind es jedoch nur 9 Kombinationen, in denen das Produkt der beiden Zahlen auf den Würfeln ungerade ist: 1 · 1; 1 · 3; 1 · 5; 3 · 1; 3 · 3; 3 · 5; 5 · 1; 5 · 3; 5 · 5. In allen anderen Würfelkonstellationen ist die Zahl mindestens eines Würfels gerade, wodurch auch das Produkt gerade ist. Das Würfelprodukt ist also in 27 von 36 Fällen gerade, was eine Gewinnchance von 75% ergibt. Das Spiel ist also tatsächlich unfair. | Download | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Die Tabelle gibt wieder, welche Zahlen mit welcher Kombination möglich sind. Wichtig: Mia kann natürlich auch (absichtlich) vorbeiwerfen! In der Tabelle ist dies mit einem X gekennzeichnet
|
Download | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Diese Aufgabe ist (vielleicht) die Mutter aller Knobelaufgaben. Laut Wikipedia ist sie schon seit fast 900 Jahren bekannt. Die Lösung wird in der Wikipedia folgendermaßen beschrieben:
Zunächst füllt man das 5-Liter-Gefäß aus dem 8-Liter-Gefäß bis zum Rand, zurück bleiben 3 Liter: (0, 5, 3) Aus dem 5-Liter-Gefäß füllt man das 3-Liter-Gefäß bis zum Rand: (3, 2, 3) Das 3-Liter-Gefäß entleert man in das 8-Liter-Gefäß: (0, 2, 6) Den Inhalt des 5-Liter-Gefäßes schüttet man in das 3-Liter-Gefäß: (2, 0, 6) Man füllt das 5-Liter-Gefäß erneut aus dem 8-Liter-Gefäß: (2, 5, 1) Man füllt das 3-Liter-Gefäß aus dem 5-Liter-Gefäß auf: (3, 4, 1) Man schüttet den Inhalt des 3-Liter-Gefäßes in das 8-Liter-Gefäß zurück: (0, 4, 4) Zu der Knobelaufgabe gibt es auch eine Internetseite, mit der man den Prozess durch Ausprobieren lösen kann: http://www.ablmcc.edu.hk/~scy/home/javascript/notes/jugs/ |
Download | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Um die Gewichte der einzelnen Obstsorten ermitteln zu können, hilft es, wenn man sich als erstes die beiden oberen "Gleichungen" ansieht und überlegt, was der Unterschied zwischen den beiden Zeilen ist. In der unteren Zeile gibt es einen Apfel mehr, wodurch das Gewicht um 510g - 330g =180g steigt. Somit wiegt ein Apfel 180g. Daraus ergibt sich direkt, dass eine Birne 300g - 180g = 150g wiegen muss.
Eine Melone und eine Birne (150g) wiegen 5 · 180g = 900g. Von den 900g muss man also 150g abziehen, um zu ermitteln, dass eine Melone 750g wiegt. |
Download | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Da Mia nur in 4er-Schritten die Treppe hinaufspringen kann, wird sie nicht auf direktem Weg zu Momo kommen. Sie muss zuerst auf eine Stufe oberhalb Momo springen, die an der Einerstelle entweder eine 7 oder eine 2 stehen hat. In 4er Schritten wird sie aber nicht auf eine Stufe kommen, deren Einerstelle "7" ist.
Der kürzeste Weg geht in 8 Sprüngen auf Stufe 32 und dann in 2 Sprüngen herunter auf die 22. Sie braucht also 10 Sprünge. |
Download | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Da sich die Zahl der Wespen in jeder Woche verdoppelt hat, muss man zur Ermittlung des Baubeginns einfach rückwärts rechnen, also so oft die Zahl 768 halbieren, bis man bei der Zahl 6 ankommt.
768 : 2 = 384 384 : 2 = 192 192 : 2 = 96 96 : 2 = 48 48 : 2 = 24 24 : 2 = 12 12 : 2 = 6 Der Nestbau hat folglich vor 7 Wochen begonnen. |
Download | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Bei der Lösung der Aufgabe hilft es, wenn man sich in einem ersten Schritt überlegt, was überhaupt passiert, wenn eine Gruppe von 4 Leuten sich gegenseitig die Hände schüttelt:
Person 1 schüttelt 3 Personen die Hände (sich selbst natürlich nicht) Person 2 schüttelt 2 Personen die Hände (mit Person 1 hatte sie bereits das Vergnügen Person 3 schüttelt 1 Person die Hände Person 4 hat schon mit jedem die Hände geschüttelt. Bei 4 Personen gibt es also 1 + 2 + 3 = 6 Schüttelvorgänge. Mit jeder Person, die dazukommt, muss nun eine weitere Zahl addiert werden. 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = 78. Dies ist jedoch die Rechnung für 13 Personen. Auf der Party schütteln sich also 13 Katzen die Hände. Da Mia selbst auch dabei ist, müssen also 12 Freunde auf der Party eingeladen sein. |
Download | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Vorweg: Bei der Lösung wird außer Acht gelassen, dass die Stoffstücke beim Nähen der Decke ein wenig überlappen sollten. Es muss also nur ein Weg gefunden werden, wie die große Fläche von 91 cm x 88 cm mit den kleinen Stücken ausgelegt werden kann. Dabei müssen die Stücke natürlich nicht in der beschriebenen Ausrichtung vernäht werden, sondern dürfen auch gedreht werden.
Für die lange Seite (91 cm) braucht man 8 Stücke mit 13 cm Breite. Für die kürzere Seite reichen dann 11 Stücke mit 8 cm Breite, so dass es insgesamt 88 Stücke Stoff sind. |
Download | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Am sichersten löst man diese AUfgabe natürlich, wenn man sich die Muster 1 bis 10 aufmalt und anschließend die Punkte/Erbsen auszählt. Dies dürfte jedoch einige Zeit in Anspruch nehmen. Schneller geht es, wenn man die arithmetische Regel für die Muster erkennt. Muster 1 besteht aus 1 · 2 Erbsen, Muster 2 aus 2 · 3 Erbsen usw. Muster 10 wird also aus 10 · 11 Erbsen bestehen. Demnach braucht Mia für ihre Muster insgesamt 440 Erbsen (2 + 6 + 12 + 20 + 30 + 42 + 56 + 72 + 90 + 110). | Download | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Aufgabe 21-20
| Aufgabe | Lehrerkommentar | PDF-Vorlage |
|---|---|---|
| Durch die Zeichnung ist diese Aufgabe relativ einfach zu lösen. Mit ihrer Hilfe lässt sich nämlich ermitteln, dass die Pyramide 8 Kanten besitzt, die alle gleich Lang sind. Für den Bau der Pyramide hat Mia 48 cm Draht (50 cm - 2 cm) verwendet. Folglich sind die Kanten 48 cm : 8 = 6 cm lang. Eine interessante Frage wäre nun, wie ich die Pyramide ist, aber für Grundschüler vermutlich nicht zu lösen :). | Download | |
| Intuitiv möchte man diese Aufgabe vielleicht mit einer Zeichnung lösen. Allerdings wird beim Betrachten des Ergebnisses klar, dass dies eine unverhältnismäßig aufwendige Aufgaben wird. Daher sind hier arithmetische Überlegungen die bessere Alternative: Da jeder der 6 dicken Äste 5 dicke Zweige hat, sind es 6 · 5 = 30 dicke Zweite, die der Baum hat. Jeder der dicken Zweige hat 4 dünne Zweige, was in der Summe 30 · 4 = 120 dünne Zweige hat. An jedem der Zweige hängen nur 2 Äpfel, was insgesamt 120 · 2 = 240 Äpfel sind. | Download | |
| Bei dieser Aufgabe geht es zu erst einmal darum, einen sinnvollen Ansatz für die Lösung zu finden. Hier ist eine Zeichnung hilfreich, die das Glockengeläut visualisiert. Um 7 Uhr wird die Glocke 7 Mal klingen, unterbrochen von 6 Pausen: O - O - O - O - O - O - O.
Da das gesamte Läuten 24 Sekunden dauert, muss jede Pause (etwa) 6 Sekunden dauern. (An dieser lassen wir einmal außer Acht, dass auch der 7. Schlag noch nachklingen wird und jeder Schlag selbst auch eine Dauer von wenigen Millisekunden hat. Um 22 Uhr sieht die Visualisierung so aus: O - O - O - O - O - O - O - O - O - O - O - O - O - O - O - O - O - O - O - O - O - O, bzw. O - O - O - O - O - O - O - O - O - O, je nachdem ob man annimmt, dass die Kirchenuhr 22 mal schlägt oder eben nur 10 mal. Entsprechend gibt es dann 21 bzw. 9 Schlagpausen. Daraus ergibt sich, dass das gesamte Geläute 54 Sekunden bzw. 126 Sekunden, also 2 Minuten und 6 Sekunden dauern wird. |
Download | |
| Bei dieser Aufgaben werden die Kinder wohl vor allem Trial-and-Error-Strategien anwenden. Um die geforderten 2 Dreiecke und 2 Vierecke zu erhalten, muss der Kuchen einmal exakt auf der Diagonalen geschnitten werden, so dass man zwei Dreiecke erhält. Danach schneidet man einmal nicht durch die Diagonale, um zwei Dreiecke und zwei Vierecke zu erhalten (die dann natürlich keine Rechtecke oder Quadrate sind, aber das war ja auch nirgends gefordert). | Download | |
| Die Lösung dürfte den Schüler*innen am einfachsten gelingen, wenn sie sich überlegen, wie lange Momo braucht, um einen kompletten Sack zu verbrauchen. Hierzu braucht er 60 Tage. In dieser Zeit verbraucht Mia 2 Säcke, so dass die beiden insgesamt in 60 Tagen 3 Säcke verbrauchen. Folglich kommen sie mit einem Sack 60 Tage : 3 = 20 Tage aus. | Download | |
| Vorab zwei Lösungen: 123 + 45 - 67 + 8 - 9 = 100 und 123 - 45 - 67 + 89 = 100
Diese Aufgabe löst man vermutlich am ehesten mit systematischen Probieren. |
Download | |
| Wenn man diese Aufgabe strukturiert angehen möchte, zerlegt man den Würfel am besten "mental" in kleinere Einheiten:
Der Würfel besteht aus 9 Dreierstangen. An einer Dreierstange gibt es 2 Paare von Berührungsflächen, so dass Mia für eine Stange zwei Punkte setzen muss. Für eine Platte (3x3 Würfel) braucht man 3 Stangen (also sechs Punkte). Beim Verbinden von zwei Stangen berühren sich immer 3 Paare von Berührungsflächen, macht also weiter 6 Klebepunkte. Pro Platte müssen also 12 Punkte gesetzt werden. Der Würfel besteht aus 3 Platten, wodurch schon 36 Klebepunkte erreicht werden. Beim verbinden zweier Platten berühren sich immer 9 Paare von Berührungsflächen. Dadurch entstehen also insgesamt 18 weitere Klebepunkte. Mia muss als insgesamt 54 Punkte setzen. |
Download | |
| Mit einer Skizze/Tabelle lässt sich diese Aufgabe recht einfach lösen. Es geht jedoch auch mit logischen Überlegungen. Der erste Streifen ist rot. Da der Schal aus 6 Farben besteht, die sich immer in der gleichen Reihenfolge wiederholen, wird auch das 7. und das 13. Feld rot sein. Demnach ist das 14. Feld orange. Hier macht Mia also ihre Pause. Der Reihe nach macht sie beim 15. Feld mit gelb weiter. | Download | |
| Für diese Aufgabe bedarf es einer kleinen Vorüberlegung: Da Mia 52 Leckerlis besitzt, sie aber am Ende eines übrig behält, hat sie nur 51 Leckerlis an ihre Kaninchen verfüttert. Die Kinder werden nun vermutlich mit systematischem Probieren vorgehen. Als Lehrer kann man die Aufgabe mit einer kleinen Gleichung lösen. Das kleinste Kaninchen bekommt x Leckerlis. Jeder weiteres Tier bekommt je ein Stück mehr. Es ergibt sich folgende Gleichung: x + x + 1 + x + 2 + x + 3 + x + 4 x + 5 = 51. Zusammengefasst ergibt sich: 6x + 15 = 51. Folglich sind 6x = 36, also X =6. Das kleinste Kaninchen hat 6 Leckerlis erhalten. | Download | |
| Für die Lösung der Aufgabe muss man zuerst ermitteln, was eine Kugel Eis kostet. Mia kann sich 3 Kugeln Eis leisten, behält sogar noch 20ct übrig. Bis zur nächsten Kugel fehlen ihr jedoch 40ct. Folglich muss eine Kugel Eis 60ct kosten. Die 3 Kugeln, die Mia sich leisten kann, kosten also 1,80€. Da sie 20ct übrig hat, hatte sie zu Beginn ihres Einkaufs 2€ bei sich. | Download |
Aufgabe 31-40
| Aufgabe | Lehrerkommentar | PDF-Vorlage |
|---|---|---|
| Die Anordnung der Kinder ist bei dieser Aufgabe eigentlich egal, so verlockt die Kinder jedoch vielleicht zu Lösungswegen mit Skizze. Mathematisch ist hier eigentlich nur die Aufgabe 36 : 8 = 4 Rest 4 zu lösen. Da am Ende ein Rest von 4 Keksen bleibt, Mia diese aber brav weiter verteilt, bekommen also 4 Freunde 5 Kekse, während 4 weitere Freunde nur 4 Kekse erhalten. | Download | |
| Insgesamt gibt es eigentlich 4 · 3 · 2 · 1 = 24 Möglichkeiten, das Blumenkistchen zu bepflanzen. Allerdings möchte ja auf jeden Fall, dass die rote Tulpe von der lila und der gelben Tulpe eingerahmt ist. Ein Teil des Kistchens ist also G - R - L oder L - R - G. Die schwarze Tulpe kann nun entweder immer links oder rechts neben dieser Gruppe stehen. Es gibt also 2 · 2 = 4 Möglichkeiten, wie Mia ihr Kistchen gestalten kann.
PS: Es gibt wirklich (fast) schwarze Tulpen: http://www.meinanzeiger.de/erfurt/natur/gibt-es-wirklich-schwarze-tulpen-d16233.html |
Download | |
| Der gesamte Turm besteht aus 3 · 3 · 7 = 63 Würfeln. Zerlegt man den Turm in seine 7 Schichten, stellt man fest, dass zwei verschiedene Arten von Schichten gibt: 4 Schichten, in denen es 5 weiße und 4 schwarze Würfel gibt und 3 Schichten, in denen es 4 weiße und 5 schwarze Würfel gibt. Somit erkennt man schnell, dass es 32 weiße Würfel und 31 schwarze Würfel sind, die Mia in ihrem Turm verwendet hat. | Download | |
| Mia hat sich insgesamt 2 · 12 = 24 Eier gekauft. Da sie 14 Eier mit blauen Streifen versieht, bleiben vorerst 10 Eier "nackt". Wenn Mia nun in einem ersten Schritt zuerst diese 10 Eier mit grünen Streifen bemalt, muss sie dann aber noch 4 weitere Eier mit grünen Streifen versehen, die aber auch schon blaue Streifen haben. Es gibt also mindestens 4 zweifarbige Eier. | Download | |
| Für die Lösung dieser Aufgabe ist es wichtig zu wissen, dass Dominosteine zwei Seiten haben und beim Legen einer Dominoreihe stets zwei gleiche Seiten aneinandergefügt werden. Folglich sind von den beiden leeren/geklauten Steinen schon zwei Felder bekannt (5 und 3). Die bisherige Gesamtsumme der Punkte beträgt inklusive dieser beiden Felder also 45. Da Mia bei der kompletten Reihe die Summe 47 gezählt hatte, müssen die beiden fehlenden Felder also jeweils mit einer 1 belegt werden. | Download | |
| Zwei Wochen haben 14 Tage. Somit wird die Sonne in 14 Tagen 28 Minuten früher aufgehen (die reale Veränderung der Sonnenaufgangszeiten ist leider nicht ganz im 2-Stunde-Rhythmus). Die Sonne geht demnach um 6:41 auf, was dann auch Mias Aufstehzeit entspricht. | Download | |
| Die Kinder werden bei der Lösung ggf. zu einer Rechentabelle greifen oder die Taschengeldbeträge schrittweise zum Ausgangsbetrag addieren. Mit einer einfachen Überlegung gelingt die Lösung der Aufgabe jedoch viel einfacher:
Mia hat zu Beginn 11€ mehr als Momo. Momo bekommt jedoch jede Woche 1€ mehr Taschengeld. Daher wird Mia ihren Vorsprung nach exakt 11 Wochen aufgebraucht haben. |
Download | |
| Intuitiv wird man mit Sicherheit denken, dass es mit zwei Würfeln einfacher ist, die Würfelsumme 6 zu erreichen. Um zu erkennen, dass dem nicht so ist, sind einige Überlegungen nötig:
Beim Würfeln mit zwei Würfeln gibt es 6 · 6 = 36 verschiedene Möglichkeiten, wie die Würfel fallen können. Davon gibt es aber nur 5 Möglichkeiten, die Summe 6 zu erreichen: 1 + 5; 2 + 4; 3 + 3; 4 + 2; 5 + 1. Die Chance beträgt als 5 von 36. Beim Würfeln mit nur einem Würfel beträgt die Chance für die 6 logischerweise 1 von 6 ... oder eben 6 von 36. Somit ist es wahrscheinlicher, mit einem Würfel die Würfelsumme 6 zu erreichen. |
Download | |
| Bei dieser Aufgabe hilft es, wenn man sich im ersten Schritt überlegt, aus wie vielen Kugeln und Streichhölzern ein Würfel besteht. Es sind 8 Kugeln (Ecken) und 12 Streichhölzer (Kanten). Die fertige Figur besteht natürlich nicht aus 4 vollständigen Würfeln, sondern eigentlich nur aus 2 vollständigen Würfeln und einigen ergänzenden Bauteilen. Es sind insgesamt 20 Ecken (=Kugeln) und 36 Streichhölzer (=Kanten). | Download | |
| Mathematisch gesprochen soll eine Summe <=20 erzeugt werden, die aus möglichst vielen unterschiedlichen Summanden besteht. 1 + 2 + 3 + 4 + 5 = 15. Es bleiben zwar 5 Eier übrig, aber die Anzahl 5 hat Mia ja schon verteilt. Sie kann also höchstens 5 Nester füllen.
Mit dieser Aufgabe geht die Knobelkartei in die Osterpause. Ab dem 24.04.2017 gibt es wieder neue Knobelaufgaben. Ich hoffe, dass ich die Kartei bis Jahresende auf 100 Aufgaben anwachsen lassen kann, ehe ich mich dann der Klasse 1/2 widmen kann. |
Download |
Aufgabe 41-50
| Aufgabe | Lehrerkommentar | PDF-Vorlage | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mia muss bei ihrem Krankenhaus höchstens 10 Türen aufsuchen. Im ersten Stock sind es die Türen 103, 130, 112, und 121. Im zweiten Stock sind es die Türen 202, 220 und 211. Im dritten Stock dann noch die Türen 301 und 300. Und natürlich könnte die Großmutter auch in Zimmer 400 liegen. | Download | |||||||||||||||||||
Aus mathematischer Sicht muss bei dieser Aufgabe eine ganzzahlige Zerlegung der Zahl 17 gefunden werden, bei der der erste Summand ein Vielfaches von drei ist und der zweite Summand ein Vielfaches von vier. Für die Lösung legt man sich am Besten eine Tabelle an, die die Vielfachen von drei auflistet:
Dann erkennt man schnell, dass Mia drei Dreiecke und zwei Vierecke gebaut haben muss! |
Download | |||||||||||||||||||
| Die Lösung dieser Aufgabe gelingt eigentlich recht zügig und einfach. Man muss jedoch eine Besonderheit bedenken: Mia zählt 25 Autos bis zum Treffpunkt, Momo 31 Autos. Nun ist man geneigt schnell zu folgern, dass es insgesamt 25 + 31 = 56 Autos sind. Allerdings haben Mia und Momo das Auto ihres Treffpunktes doppelt gezählt. Es sind also insgesamt nur 56 - 1 = 55 Autos in der Schlange. | Download | |||||||||||||||||||
| Die Gartenarbeit von Mia lässt sich in eine einfache Gleichung übertragen: 3x + x = 52 (wobei X hierbei für die Anzahl der Möhren steht). Folglich sind 4x = 52 oder eben x = 13.
Die Kinder werden vermutlich nicht auf die Idee kommen, eine Gleichung aufzustellen. In diesem Fall kann eine Rechentabelle helfen. |
Download | |||||||||||||||||||
| Um die Gesamtspieldauer des Hörbuchs zu ermitteln, muss mit Zeitangaben gerechnet werden, was für Kinder in der Regel ungewohnt ist, da hier nicht das Dezimale Stellenwertsystem ausgenutzt werden kann.
Die erste Geschichte hat eine Spieldauer von 425 Sekunden. Dies entspricht 7 Minuten und 5 Sekunden. Diese Dauer lässt sich geschickt mit der Dauer der dritten Geschichte addieren. Zusammen laufen diese beiden Geschichten für 14 Minuten. Addiert man hierzu noch die Länge der zweiten Geschichte, ergibt sich eine Gesamtspieldauer von 18 Minuten und 13 Sekunden. |
Download | |||||||||||||||||||
| Da Mia ein Jahr älter ist als Momo, wird Momo seinen 9. Geburtstag erst im Jahr 2018 feiern. Da Mia zudem noch 7 Tage älter ist, feiert Momo seinen Geburtstag auch 7 Tage später, also am 9.5.2018. Das Hauptproblem für die Kinde dürfte sein, in welche Richtung man denken/rechnen muss. | Download | |||||||||||||||||||
| Zwischen der Gondel von Mia und Momo liegen auf einem Halbkreis 6 weitere Gondeln (4, 5, 6, 7, 8 und 9). Also müssen müssen auch auf dem zweiten Halbkreis 6 weitere Gondeln sein. Zwei dieser Gondeln müssen die Nummer 1 und 2 tragen. Folglich bleiben vier Gondeln, die die Nummern 11, 12, 13 und 14 tragen. Hilfreich ist bei der Lösung dieser Aufgabe eine Zeichnung. | Download | |||||||||||||||||||
| Die folgende Figur besteht aus 7 · 7 = 49 Fliesen, wobei es 3 · 3 = 9 Lücken geben wird. Folglich braucht Mia für die 3. Figur 40 Fliesen. | Download | |||||||||||||||||||
| Für 8 Brötchen muss Mia 8 · 0,36€ = 2,88€ bezahlen. Sie behält also 2,12€ übrig. Von diesem Geld kann sie 9 Kekse kaufen, für die sei dann 2,07€ bezahlen muss. 5ct behält Mia übrig. | Download | |||||||||||||||||||
| Folgende Palindromzahlen liegen zwischen 191 und 323: 202, 212, 222, 232, 242, 252, 262, 272, 282, 292, 303, 313. Es sind 12 Zahlen. | Download |
Aufgabe 51-60
| Aufgabe | Lehrerkommentar | PDF-Vorlage | |||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Da Mia möglichst wenig tragen möchte, ist sie bestrebt, möglichst viele Kartons mit 12 Eiern zu kaufen. Mit 6 Kartons kann sie auf diese Weise 72 Eier erwerben. Für die beiden fehlenden Eier kann sie entweder einen 6er, aber auch einen 12er Karton kaufen. In jedem Fall braucht sie 7 Kartons. | Download | ||||||||||||||||||||||||||||||||||||||||
| Dies ist die erste Knobelaufgabe der Kartei, die nicht zu lösen ist. Mia und Momo haben von Mias Onkel insgesamt 89 Gummibärchen erhalten. Da dies eine ungerade Anzahl ist, ist keine gerechte Verteilung möglich. | Download | ||||||||||||||||||||||||||||||||||||||||
| Die nächste Zahl, bei der alle 5 Ziffern verschieden sind, ist die Zahl 84560. Bis dorthin muss Mias Mutter noch 84560 - 84539 = 21 Kilometer fahren. | Download | ||||||||||||||||||||||||||||||||||||||||
| Der einfachste Lösungsweg für diese Aufgabe ist natürlich der, bei dem man alle Zahlen von 1 bis 20 aufschreibt und zählt, wie oft die Ziffer 1 vorkommt. Man könnte aber auch den Aufbau des Zahlensystems ausnutzen. Von 0 bis 9 und von 10 bis 19 kommt die 1 jeweils einmal an der Einerstelle vor. Von 10 bis 19 kommt zu sie zudem zehnmal an der Zehnerstelle vor. Somit muss Mia 12 Exemplare der Ziffer 1 kaufen. | Download | ||||||||||||||||||||||||||||||||||||||||
| Der erste Kurs findet am 10. Mai statt. Folglich sind die weiteren Termine im Mai am 17., 24. und 31. Mai. Zwei Termine finden dann noch im Juni statt: 7. und 14. Juni. Somit endet der Kurs am 14. Juni. Ob Mia bis dahin schwimmen gelernt hat? | Download | ||||||||||||||||||||||||||||||||||||||||
| Gesucht werden müssen Divisionsaufgaben mit dem Dividenden 33, bei denen der Rest 3 bleibt. Dies sind folgende Aufgaben:
33 : 5 = 6 Rest 3 33 : 6 = 5 Rest 3 33 : 10 = 3 Rest 3 33 : 15 = 2 Rest 3 33 : 30 = 1 Rest 3 |
Download | ||||||||||||||||||||||||||||||||||||||||
| Zur Lösung wird es am einfachsten sein, wenn man sie das dritte Muster dazumalt. Das erste Muster hat 5 schwarze Quadrate. Das zweite Muster besteht schon aus 9 Quadraten. Das dritte Muster besteht aus 17 Quadraten. | Download | ||||||||||||||||||||||||||||||||||||||||
Ein eleganter Lösungsweg ist hier mit Sicherheit das Anlegen einer Tabelle mit den Anfangszeiten der Hörspiele. Anhand der Tabelle ist die richtige Lösung dann schnell abzulesen.
Somit läuft um 14:25 Uhr noch die fünfte Folge aus Mias Hörspielmarathon. |
Download | ||||||||||||||||||||||||||||||||||||||||
| Auf den ersten Blick erscheint diese Aufgabe vielleicht besonders schwer. Als (einigermaßen geübter) Mathematiker ist man ggf. geneigt, diese Aufgaben mit zwei Gleichungen zu lösen. Dabei geht es mit ein wenig logischem Denken viel einfacher:
Hätte Mia an jedem der 30 Tage zwei Aufgaben erfunden, hätte sie nun 60 Aufgaben. Sie hat jedoch erst 59 Aufgaben erfunden, so dass sie sich an genau einem Tag nur eine Aufgabe ausgedacht hat. |
Download | ||||||||||||||||||||||||||||||||||||||||
|
Bei der Lösung dieser Aufgabe hilft es, wenn man sich die Zahlen der 7er-Reihe aufschreibt und anschließend überlegt, welche darauf folgende Zahl zur 5er-Reihe gehört. Diese Zahlen müssen dann die Altersangaben der drei Frauen sein:
|
Download |
Aufgabe 61-70
| Aufgabe | Lehrerkommentar | PDF-Vorlage | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Die Lösung der Aufgabe springt den Schüler*innen vermutlich nicht direkt ins Auge, weil 50 Minuten kein Vielfaches von 20 Minuten ist. Man kann also die Fahrleistung der beiden Katzen nicht auf direktem Wege vergleichen. Dafür muss man erst ermitteln, welche Distanz Mia in 10 Minuten schafft. Dies sind 3 Kilometer. Folglich wird Mia in 50 Minuten 5 · 3km = 15km zurücklegen. Damit ist Mia ein bisschen schneller also Momo. Profis möchten vielleicht sogar die genaue Geschwindigkeit ausrechnen: Mia fährt in einer Stunde 6 · 3km =18km, schafft also 18 km/h. Momo fährt in 10 Minuten 2,8km, schafft also in einer Stunde 16,8km, was einer Geschwindigkeit von 16,8km/h entspricht. | Download | ||||||||||||||||||||||||||||||||||||||||||||||
| Vorab die richtige Lösung: Mias Onkel Manuel ist 45 Jahre alt, denn 45 + 4 + 5 = 54. Die Kinder werden dies am ehesten durch ausprobieren herausbekommen. Die mathematische Herleitung ist ein wenig komplexer:
Aus den Bedingungen der Aufgabe ergibt sich folgende Gleichung: 10a + b + a + b = 10b + a Diesen Term kann man Umwandeln, auflösen und zusammenfassen zu 5a = 4b, wobei für a und b nur ganzzahlige Werte in Frage kommen. Dies passt nur, wenn a=4 und b=5 sind, wodurch sich dann die Zahlen 45 und 54 ergeben. Kinder werden diesen Weg mit Sicherheit nicht gehen :) |
Download | ||||||||||||||||||||||||||||||||||||||||||||||
| Diese Aufgabe hat eine gewisse Ähnlichkeit zu dem 3-Krüge-Problem. Zuerst muss Mia beide Uhren umdrehen. Wenn die 3-Minuten-Uhr abgelaufen ist, dreht Mia diese erneut um. In der 5-Minuten-Uhr sind jetzt noch 2 Restminuten übrig. Wenn diese Restminuten abgelaufen sind, dreht sie 5-Minuten-Uhr erneut um. In der 3-Minuten-Uhr laufen nun noch 60 Sekunden ab. Wenn diese verstrichen sind, sind in der 5-Minuten-Uhr noch 4-Minuten Restsand. Somit kann Mia dann exakt 4 Minuten abmessen. | Download | ||||||||||||||||||||||||||||||||||||||||||||||
|
Hier dürfte eine Tabelle bei der Lösung hilfreich sein:
|
Download | ||||||||||||||||||||||||||||||||||||||||||||||
| Der schnellste Weg zur Lösung dieser Aufgabe ist das systematische Ausprobieren. In diesem Fall legt man dafür die Länge einer Fahnenseite fest und sieht sich an, welchen Wert dann die andere Seite annehmen müsste.
Nehmen wir an, die erste Seite wäre nur eine Meter lang. Die zweite Seite nennen wir b. Dann wäre (1 + 1 + b + b) · 9,50 + 1 · b · 7 = 137. b wäre dann 4,538 .... als auf jeden Fall kein ganzzahliger Wert. Nehmen wir an, die erste Seite wäre nun zwei Meter lang. Die zweite Seite nennen wir b. Dann wäre (2 + 2 + b + b) · 9,50 + 2 · b · 7 = 137. b wäre dann 3. Somit ist eine ganzzahlige Lösung gefunden. |
Download | ||||||||||||||||||||||||||||||||||||||||||||||
| Intuitiv denkt man wohl schnell, dass die größte Summe um 23:59:59 erreicht wird. Die größte Ziffernsumme der Sekunden und Minuten erreicht man mit der Zahl 59 (5 + 9 = 14). Die größte Summer bei den Stunden erreicht man jedoch nicht um 23 Uhr (2 + 3 = 5). Um 19 Uhr jedoch ist die Summe der Stundenziffern 10. Somit kann eine Gesamtsumme von 38 erreicht werden. | Download | ||||||||||||||||||||||||||||||||||||||||||||||
| Das Gebäude ist insgesamt 7 Würfelchen breit, 3 Würfel hoch und 3 Würfel tief. Die Maße das Paketes müssen als insgesamt 63 cm (Breite), 27 cm (Höhe) und 27 cm Tiefe sein. | Download | ||||||||||||||||||||||||||||||||||||||||||||||
| Diese Aufgabe schließt direkt an die Aufgabe Nr. 67 an. Hier muss das Würfelgebäude nun mental zerlegt werden, um die Gesamtzahl der Würfel zu bestimmen, da nicht alle Würfel aus dieser Perspektive sichtbar sind.
In der obersten Schicht liegen 3 + 3 = 6 Würfel. In der mittleren Schicht sind es 7 + 3 = 10 Würfel. In der untersten Schicht sind es 7 + 5 + 3 = 15 Würfel. Insgesamt sind es also 31 Würfel. Da ein Würfel 18g wiegt, wiegt das gesamte Würfelgebäude 18g · 31 = 558g. Inklusive des Kartons wiegt das gesamte Paket also 688g. |
Download | ||||||||||||||||||||||||||||||||||||||||||||||
| In Mias Klasse sind insgesamt 29 Kinder. 3 Kinder haben kein Haustier, also haben 29 - 3 = 26 Kinder wenigstens einen Hamster oder ein Meerschweinchen. 14 Kinder haben einen Hamster. Daher haben 26 - 14 = 12 Kinder auf jeden Fall ein Meerschweinchen, denn sonst hätten ja noch mehr Kinder kein Haustier. Insgesamt gibt es 19 Kinder mit Meerschweinchen. Daher müssen 19 - 12 = 7 Kinder, die schon einen Hamster haben, wohl auch ein Meerschweinchen haben. | Download | ||||||||||||||||||||||||||||||||||||||||||||||
| Wenn Manuel bei der ersten Fahrt unbedingt vorne sitzen möchte, kann er entweder, mit Mia, Momo oder Marcel fahren. Das wären drei Kombinationen. Allerdings ist natürlich nicht gesagt, dass Manuel auch die erste Fahrt machen muss. Es könnten auch Mia/Marcel (oder Marcel/Mia), Mia/Momo (oder Momo/Mia) oder Marcel/Momo (oder Momo/Marcel fahren). Das wären 6 weitere Kombinationen, so dass insgesamt 9 Varianten in Fragen kommen. | Download |
Aufgabe 71-80
| Aufgabe | Lehrerkommentar | PDF-Vorlage | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wenn die 4 Kinder zusammen 12 Sammelkarten haben und Mia 4 Karten besitzt, dann haben Marcel, Manuela und Momo zusammen 8 Karten. Gesucht wird also eine additive Zerlegung der Zahl 8 mit 3 Summanden, wobei sich die 3 Summanden voneinander unterscheiden müssen und kein Summand 0 ist.
Die einzige infrage kommenden Zerlegungen ist 5 + 1 + 2 = 8. Da Momo die meisten Karten besitzt, muss er also 5 Karten haben. |
Download | |||||||||||||||||||||||||||||||||
| Diese Aufgabe ist (ausnahmsweise einmal) recht simpel zu lösen. Mia hatte 20 - 17 = 3 Fehlwürfe. Da Momo dreimal so oft verfehlt hat, sind es bei ihm 9 Fehlwürfe und ebenso 17 Treffer. Er hat also 26 Wasserbomben geworfen. | Download | |||||||||||||||||||||||||||||||||
| Mia beginnt bei der Fütterung mit den Kaninchen. Für die 3 Tiere gibt es 3 · 2 · 1 = 6 Möglichkeiten, diese in einer Reihenfolge zu bringen. Anschließend sind die Meerschweinchen dran. Für diese gibt es zwei Möglichkeiten. Nun kann Mia nach jeder "Kaninchen-Reihenfolge" noch zwischen den beiden "Meerschweinchen-Reihenfolgen" wählen, so dass es insgesamt 6 · 2 = 12 Varianten gibt. | Download | |||||||||||||||||||||||||||||||||
| Wenn Mia der Kassiererin einen 20€-Schein überreicht und 1€ zurückbekommt, dann hat ihr Einkauf wohl 19€ gekostet. Hätte Mia nur Dahlien und Hortensien gekauft, dann wäre der Wert ihres Einkaufs immer eine gerade Zahl. Somit muss Mia mindestens eine Geranie gekauft haben. | Download | |||||||||||||||||||||||||||||||||
| Bei der Lösung der Aufgabe muss beachtet werden, dass hier nicht die Anzahl der zu tragenden Gegenstände wichtig ist, sondern deren Gewicht. Alle Zutaten zusammen wiegen 950g, so dass für die beiden Katzen je 475g zu tragen wären. Auch wenn nicht explizit danach gefragt ist, gibt es natürlich verschiedene Möglichkeiten ... doch dazu gibt es dann morgen eine Aufgabe. | Download | |||||||||||||||||||||||||||||||||
|
Es gibt zwei Möglichkeiten, wie Mia und Momo die Einkäufe gerecht nach Hause tragen können:
|
Download | |||||||||||||||||||||||||||||||||
| Wenn Mias Mutter dreimal so viele Erdbeeren wie Mias Mutter hat, dann haben beide zusammen vier Anteile Erdbeeren: Mia hat einen Anteil und die Mutter drei Anteile. Wenn man also das Gesamtgewicht durch 4 dividiert, erhält man das Gewicht von Mias Anteil. 1832 : 4 = 458g
Mia hat also 458g Erdbeeren gepflückt (bzw. ist ihr Korb so schwer). |
Download | |||||||||||||||||||||||||||||||||
| Bei dieser Aufgabe müssen die beiden Schrägansichtern der Wasserbombentürme mental zerlegt werden, um die jeweilige Gesamtzahl der gestapelten Wasserballons zu ermitteln. Schließlich müssen diese dann noch verglichen werden.
Momo: Momos Stapel besteht in der untersten Schicht aus einem 3x3-Quadrat, in der mittleren Schicht aus einem 2x2-Quadrat und oben aus einem einzelnen Ballon. Es sind also 9 + 4 + 1 = 14 Ballons. Mia: Mias Stapel besteht aus Dreicken. das unterste Dreieck besteht aus 4+3+2+1=10 Ballons. Das zweite Dreieck aus 3+2+1=6 Ballons. Das dritte Dreieck aus 2+1=3 Ballons und zuoberst liegt ein weiterer Ballon. Es sind also 10 + 6 + 3 + 1 = 20 Ballons. Mia hat also 6 Wasserbomben mehr! |
Download | |||||||||||||||||||||||||||||||||
| Die Kurzfassung der Lösung ist: in die Momos Schachtel passen 6-mal so viele Kirschen hinein. Diese Einsicht erreicht am ehesten, wenn man konkrete Zahlen für Mias Schachtel annimmt. Legt man beispielsweise fest, dass die Schachtel 10cm hoch, 10cm breit und 10cm tief ist, so hat sie ein Volumen von 10cm · 10cm · 10cm = 1000 cm³. Momos Schachtel ist dann jedoch 30cm · 20cm · 10cm = 6000cm³ groß, also 6-mal so groß. | Download | |||||||||||||||||||||||||||||||||
|
Der sicherste Weg zur Lösung dieser Aufgabe ist eine Rechentabelle, auch wenn dieser Weg natürlich recht langwierig ist. Man kann zu der Aufgabe diese Tabelle anlegen:
Natürlich kann man auch einen direkteren Weg zur Lösung gehen: Jedes Schaf hat 1 Kopf und 4 Beine. Die Differenz zwischen der Anzahl der Köpfe und Beine ist also immer 3. Die Differenz auf der Weide nun 21 ist, müssen wohl 21 : 3 = 7 Schafe auf der Weide stehen. |
Download |
Aufgabe 81-90
| Aufgabe | Lehrerkommentar | PDF-Vorlage |
|---|---|---|
| Mia legt mir ihren Erbsen Dreiecks- und Quadratzahlen. Die Reihe der Quadratzahlen lautet 1, 2, 4, 9, 16, 25, 36, 49, ... . Die Reihe der Dreieckszahlen lautet 1, 3, 6, 10, 15, 21, 28, 36, 45, ...
Mia wird also bei der 6. Quadratzahl und der 8. Dreieckszahl merken, dass ihre Formen aus der gleichen Anzahl Erbsen bestehen. |
Download | |
| Wenn Mia auf dem ersten Foto 5 Beine fotografiert hat, dann sind im Gehege höchstens 5 Flamingos, denn 6 Flamingos würden auf mindestens 6 Beinen stehen müssen (es sei denn, ein Flamingo fliegt gerade weg).
Da Mia auf einem Foto aber 9 Beine sieht, müssen aus auch mindestens 5 Flamingos sein. 4 Flamingos haben zusammen höchstens 8 "ausgeklappte" Beine. Somit ist klar, dass im Gehege 5 Flamingos stehen. |
Download | |
| Für Kombinatorik-Profis ist diese Aufgabe recht einfach: Für Hamster 1 gibt es 4 Möglichkeiten der Namensgebung. Nachdem man diesen Namen festgelegt hat, gibt es für Hamster 2 noch 3 Möglichkeiten (da ein Name nun vergeben ist). Für den Hamster 3 gibt es dann nur noch zwei Varianten, während der letzte Hamster immer den Namen bekommt, der übrig bleibt. Dadurch gibt es 4 · 3 · 2 · 1 = 24 Möglichkeiten, wie Mia die Hamster benennen kann.
Die Schüler*innen könnten sich als Unterstützung 4 Hamster aufmalen oder mit Spielfiguren darstellen und Namensschildchen verschieben, um alle Varianten zu finden. |
Download | |
| Bei dieser Aufgabe handelt es sich eigentlich schon fast um eine klassische Sachaufgabe, die aber durch die Vielzahl an Informationen und die verschiedenartigen Rechenschritte besonders schwierig wird. Was muss im Einzelnen getan werden?
Das Volumen des Pools muss berechnet werden: 3m · 2m · 1m = 6m³ = 300cm · 200cm · 100cm = 6.000.000 cm³ = 6000 Liter Die Füllzeit muss berechnet werden: 6000 Liter : 20 Liter/Minuten = 300 Minuten = 5 Stunden Die Ende der Füllzeit muss berechnet werden: 12.00 Uhr + 5 Stunden = 17.00 Uhr |
Download | |
| Mia kommt erst um 17.10 Uhr zum Training. Sie knickt zwar um 17.55 Uhr am, ihr Training wäre aber eigentlich erst um 17.55 Uhr + 10 Minuten = 18.05 Uhr zu Ende gewesen. Seit 17.10 Uhr sind bis dahin 55 Minuten vergangen.
Da Mia aber erst zur Mitte des Trainings gekommen ist (um 17.10 Uhr), hat das Training also 55 Minuten früher begonnen. 17.10 Uhr - 55 Minuten = 16.15 Uhr. Ihr Training hätte also um 16.15 Uhr begonnen! |
Download | |
| Wenn der Monatserste ein Donnerstag ist, dann ist der 28. des Monats ein Mittwoch. Bis dahin sind vier viele Wochen vergangen, die jeweils 5 Schultage haben. Es sind also 20 Schultage gewesen. Der 29. wäre wieder ein Donnerstag und somit der 21. Schultag. Der 30. wäre ein Freitag und der 22. Schultag. Ganz gleich ob wir nun einen Monat mit 30 oder 31 Tagen haben ... der 31. wäre auf jeden Fall ein Samstag und damit schulfrei. Mia kauft sich also 22 Brötchen, wobei Brötchen 6, 12 und 18 kostenfrei sind. Also muss sie nur 19 Brötchen bezahlen. | Download | |
| Wenn Mia an 60 Tagen je eine Aufgabe gelöst hat und an 25 Tagen sogar ja zwei Aufgaben geschafft hat, dann hat sie an zusammen 85 Tagen schon 110 Aufgaben geschafft. Es bleiben also 140 - 110 = 30 Aufgaben übrig, die sie immer in Dreierbündeln gelöst hat. Dafür wird sie dann 10 Tage benötigt haben. Sie hat also bisher an 85 + 10 = 95 Tagen geknobelt. | Download | |
| Aus rein mathematischer Sicht lässt sich diese Aufgabe wieder mit zwei Gleichungen und zwei Unbekannten lösen (Zweierzimmer = x; Dreierzimmer =y):
x + y = 32; 2x + 3y = 81 => x = 32 - y; 2(32 - y) + 3y = 81 => x = 32 - y; 64 - 2y + 3y =81 => x = 32 - y; y = 17 => x = 32 - 17 = 15 Es gibt also 15 Doppel- und 17 Dreierzimmer. Schüler kommen wohl mit systhematischem Probiern am besten voran. Man legt eine Zahl für die Doppelzimmer fest und schaut dann, wie viele Dreierzimmer sich dann ergeben. |
Download | |
| Um eine sinnvolle Lösung zu entwickeln, sollte man zuerst überlegen, wie viel Flüssigkeit in allen 15 Flaschen insgesamt vorhanden ist. Dies sind 5 · 100ml + 5 · 400ml + 5 · 700ml = 6000ml. Folglich muss jede Katze 5 Flaschen mit insgesamt 2000ml Flüssigkeit bekommen.
Folgende Aufteilungen sind möglich: 700ml + 700ml + 400ml + 100ml + 100ml = 2000ml 700ml + 700ml + 400ml + 100ml + 100ml = 2000ml 700ml + 100ml + 400ml + 400ml + 400ml = 2000ml |
Download | |
| Diese Sachaufgabe muss in mehreren Schritten gelöst werden. Zuerst muss ermittelt werden, wie viele Tonpapierbögen Mia braucht. Aus einem Bogen kann Mia (wenn sie geschickt ist), 10 Einladungen schneiden (70cm : 14cm = 5; 50cm : 25cm = 2; 2 · 5 = 10).
Mia muss also 4 Bögen kaufen, um 34 Einladungen basteln zu können. 4 Bogen kosten 4 · 0,75€ = 3,00€ Mia muss also 3,00€ ausgeben. |
Download |
Aufgabe 91-100
| Aufgabe | Lehrerkommentar | PDF-Vorlage | ||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Hier wird eine Zahl gesucht, die sowohl ein Vielfaches von 8, als auch ein Vielfaches von 6 ist, bei Division durch 7 aber einen Rest von 5 lässt. Diese findet man unter anderem, wenn man sich folgende Tabelle erstellt:
Folglich ist 96 die kleinste Zahl, die alle drei Bedingungen erfüllt. |
Download | |||||||||||||||||||||||||||||||||||||||||||
|
Die Kinder werden bei dieser Aufgabe (wenn sie sie gelöst haben) von dem rasanten Wachstum erstaunt sein. Der Text wird ggf. nicht sofort verstanden. Jede Katze erzählt abends 3 neuen Katzen von dem See. Am Tag darauf gehen alle Katzen zum See: Die, die bereits am Vortag da waren und die, die neu von dem See erfahren haben. Auch hier hilft eine Tabelle:
Am Sonntag kommen also 4096 Katzen zum See ... hätte Mia mal lieber den Mund gehalten ;). |
Download | |||||||||||||||||||||||||||||||||||||||||||
| Die Pyramide, die Mia bauen will, besteht aus den ersten 5 Dreieckszahlen (1, 3, 6, 10, 15), also aus 1 + 3 + 6 + 10 + 15 = 35 Ballons.
Mia hat (wie man bereits sieht) 19 Ballons gestapelt, so dass noch 35 - 19 = 16 Ballons fehlen. |
Download | |||||||||||||||||||||||||||||||||||||||||||
| Bei dieser Aufgabe ist die Begründung von besonderer Bedeutung, denn ein "ja" oder ein "nein" ist als Antwort ja auch mal schnell geraten. Um zu ermitteln, ob das Papier für das Geschenk passt, kann zum Beispiel über eine Abwicklung des Kartons in ein Netz geschehen. In der Grafik ist ein solches Netz dargestellt. Die Außenmaße dieses Netztes übersteigen sowohl die Breite, als auch die Länge des Geschenkpapiers.
Nun könnte man natürlich noch anbringen, dass es ja mehrer mögliche Netze zum diesem Körper gibt. Diese alle zu untersuchen dauert in der Tat recht lange. Um die letzten Zweifel auszuräumen, kann man sich also den Flächeninhalt der 6 Seitenflächen ansehen. Diese sind: 20cm · 10cm = 200cm² (taucht zweimal auf) 20cm · 15cm = 300cm² (taucht zweimal auf) 10cm · 15cm = 150cm² (taucht zweimal auf) Der gesamte Flächeninhalt beträgt also 1300cm². Das Stück Geschenkpapier kommt jedoch insgesamt nur auf 1200cm². Es wird also keinesfalls passen. |
Download | |||||||||||||||||||||||||||||||||||||||||||
| Diese Aufgabe lässt sich natürlich mit (7) Kindern nachspielen. Die erste Spielerin muss 6 Mitspielerinnen umarmen. Für die zweite Spielerin bleiben dann noch 5 Mitspielerinnen übrigen, denn mit der ersten Spielerin gab es ja bereits eine Umarmung. Dies lässt sich munter fortführen. Die siebte und letzte Spielerin wurde dann bereits von allen Mitspielerinnen umarmt. Somit gibt es 6 + 5 + 4 + 3 + 2 + 1 + 0 = 21 Umarmungen nach dem Spiel. | Download | |||||||||||||||||||||||||||||||||||||||||||
|
Diese Aufgabe gibt es in unzähligen Variationen. Mit einer Tabelle lässt sich am besten deutlich machen, welches die korrekte Lösung ist:
Am Abend des 13. Tages ist Mia also bei 4 Metern angekommen. |
Download | |||||||||||||||||||||||||||||||||||||||||||
| Den Kindern wird bei der Lösung der Aufgabe hoffentlich schnell klar sein, dass die beiden Katzen zusammen weniger als eine Stunde brauchen werden. Dann werden sie ggf. versuchen zu ermitteln, wie viel Garten die Katzen z.B. in einer halben Stunde schaffen und dann ggf. schrittweise die Arbeitszeit erhöhen. Es gibt jedoch ein viel einfacheren Weg, für den man aber ein wenig um die Ecke denken muss:
Mia schafft in 2 Stunden einen Garten. Momo würde in dieser Zeit 2 Gärten schaffen. Zusammen schaffen die Katzen also in 120 Minuten 3 Gärten. Für einen Garten brauchen sie dann also 120min : 3 = 40min. Gemeinsam können sie die Arbeit also in 40 Minuten erledigen. |
Download | |||||||||||||||||||||||||||||||||||||||||||
| Wenn Mia inzwischen bei Seite 96 angelangt ist, dann hat sie 96 : 6 = 16 "Päckchen" á 9 Minuten gelesen, also ingesamt 144 Minuten gelesen. Momo schafft in dieser Zeit 144 : 6 = 24 Päckchen á 6 Minuten. In jedem Zeitraum von 6 Minuten liest er 5 Seiten, also er nun schon 24 · 5 = 120 Seiten gelesen. | Download | |||||||||||||||||||||||||||||||||||||||||||
| Auch bei dieser Aufgabe muss man ein wenig um die Ecke denken, damit man sich nicht in komplizierten Rechnungen verzettelt. Es lohnt sich zu überlegen, was der Unterschied zwischen Einkaufsmöglichkeit 1 und 2 ist. Für 3 Schokoriegel und 2 Bonbons weniger bekommt Mia 3 Sticker mehr. Lässt Mia also bei der zweiten Variante wiederum 3 Riegel und 2 Bonbons weg, würde sie dafür ebenfalls 3 Sticker mehr bekommen. Dann hätte sie 13 Sticker, dafür aber keine Bonbons und Riegel. | Download | |||||||||||||||||||||||||||||||||||||||||||
| Der Satz, den Mia aufschreiben möchte, hat 22 Buchstaben. Folglich kann Mia ihn 45-mal aufschreiben und schafft damit schon 990 aufgeschriebene Buchstaben. Bis zur 1000 sind es dann noch 10 Buchstaben. Der 10. Buchstabe des Satzes ist das n. Somit schreibt Mia als 1000. Buchstaben das "n" auf. | Download |
Material