Knobeln mit Mieze Mia
"Knobeln mit Mieze Mia" ist eine gemeinschaftliche entwickelte Knobelkartei unter offener Nutzungslizenz.
Gemeinschaftlich entwickelt
Zur Knobelkartei werden alle Quelldateien mitveröffentlich. Daher sind alle interessierten Nutzer aufgerufen, an der Weiterentwicklung der Kartei mitzuwirken. Vorschläge für neue Aufgaben können auf dieser Seite eingereicht werden. Dabei spielt es keine Rolle, ob die Aufgaben schon die Vorlage eingefügt sind oder nur als Text in der Mail umschrieben werden.
Offene Nutzungslizenz
Die Aufgaben und Materialien der Knobelkartei sind unter einer creative-commons-Lizenz veröffentlicht. Dies ermöglicht allen Nutzern folgende Rechte
- Teilen — das Material in jedwedem Format oder Medium vervielfältigen und weiterverbreiten
- Bearbeiten — das Material remixen, verändern und darauf aufbauen und zwar für beliebige Zwecke, sogar kommerziell.
Der Lizenzgeber kann diese Freiheiten nicht widerrufen solange Sie sich an die Lizenzbedingungen halten. Dabei geltende folgende Bedingungen:
- Namensnennung — Sie müssen angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade Sie oder Ihre Nutzung besonders.
- Weitergabe unter gleichen Bedingungen — Wenn Sie das Material remixen, verändern oder anderweitig direkt darauf aufbauen, dürfen Sie Ihre Beiträge nur unter derselben Lizenz wie das Original verbreiten.
Vollständiger Lizenztext unter: https://creativecommons.org/licenses/by-sa/4.0/legalcode.de
Sowohl die PDF-Dateien, als auch die Quelldateien, als auch die Bilddateien dürfen (und sollen) z.B. auf Schulhomepages oder an anderer Stelle veröffentlicht werden.
Überlegungen zum Einsatz im Unterricht
Um die noch immer stetig wachsende Knobelkartei im Unterricht zu nutzen, gibt es verschiedene Möglichkeiten. Hier kommt ein erster Vorschlag:
Bei einer zweiten Variante der Aufgabenkarten sind diese wesentlich kleiner gehalten, so dass sie auf selbstklebende Etiketten in DIN-A7 passen. Hierzu haben ich auch eine PDF-Vorlage erstellt, bei der entweder pro Aufgabe ein Etikett und pro Aufgabe eine ganze Seite Etiketten verwendet wurde. Dazu begleitend gibt es eine Druckvorlage für ein Mia-Heft, in das man die Etiketten passgenau einkleben kann. Auf der Seite gibt es dann zusätzlich ein Feld mit Rechenkästchen, ein Blankofeld und ein Feld für die Antwort und die Erklärung des Lösungswegs.
Die Etiketten kann man (ggf. schon geschnitten) in einem Karteikasten o.ä. bereitstellen. Die Schüler*innen können sich dann (in Freiarbeitsphasen etc.) ein Etikett nehmen und dies in ihr Heftchen einkleben, um dann individuell an der Aufgabe zu arbeiten.
Twitterkanal
tbc.
Aufgaben Klasse 3/4
<popup name="Aufgabe 1-10">
| Aufgabe | Lehrerkommentar | PDF-Vorlage | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Diese kombinatorische Aufgabe ist vergleichsweise einfach zu lösen. Für den ersten Würfel gibt es 6 verschiedene Möglichkeiten zu fallen (1 - 6), für den zweiten Würfel ebenfalls. Demnach gäbe es eigentlich 6 · 6 = 36 Möglichkeiten. Hier greift jedoch die Einschränkung, dass nur verschiedene Würfelergebnisse gezählt werden sollen. Die Ergebnisse "1 und 6", sowie "6 und 1" sind in diesem Sinne identisch und werden als ein Ergebnis gewertet. Somit bleiben 21 verschiedene Möglichkeiten übrig:
1 + 1; 1 + 2; 1 + 3; 1 + 4; 1 + 5; 1 + 6; 2 + 2; 2 + 3; 2 + 4; 2 + 5; 2 + 6; 3 + 3; 3 + 4; 3 + 5; 3 + 6; 4 + 4; 4 + 5; 4 + 6; 5 + 5; 5 + 6; 6 + 6 Die Schülerinnen und Schüler werden am ehesten mit einem strukturierten Vorgehen auf die vollständige Lösung kommen: Erst alle Würfelergebnisse mit 1, dann alle Würfelergebnisse mit 2, ..., am Ende alle doppelten Ergebnisse streichen. In diese Richtung könnten auch mögliche Hilfestellungen gehen. |
Download | |||||||||||||||||||
| Diese geometrische Aufgabe lässt sich auf zwei Weisen lösen: kopfgeometrisch, indem man sich den Faltvorgang vorstellt oder enakitv, indem die Faltvorlagen ausgeschnitten und zusammengefaltet werden.
Falsch ist jedenfalls die Vorlage 3, denn die beide Flächen ganz rechts überdecken sich beim Falten, so dass der entstehende Würfel an einer Seite offen ist. |
Download | |||||||||||||||||||
| Diese Aufgabe gehört im Grunde in die Kategorien Arithmetik und Kombinatorik. Gesucht wird eine vierstellige Zahl. Bei der Beschreibung wurde bewusst auf die Verwendung der Stellenwertbezeichnungen (Einer, Hunderter, ...) verzichtet, da Nummern eines Fahrradschloss in der Regel als Set von Einzelziffern ausgesprochen werden. Bei der Lösung empfiehlt es sich, von der dritten Stellen ausgehend zu überlegen und dann nach und nach zu überlegen, was daraus für die zweite und erste Stelle folgt:
Dritte Stelle 1 -> Zweite Stelle 2 -> Erste Stelle 4 Dritte Stelle 2 -> Zweite Stelle 4 -> Erste Stelle 6 Dritte Stelle 3 -> Zweite Stelle 6 -> Erste Stelle 8 Dritte Stelle 4 -> Zweite Stelle 8 -> Erste Stelle 10 -> nicht möglich An vierter Stelle kann nur eine ungerade Ziffer stehen (1, 3, 5, 7, 9). Da es die Zusatzbedingung gibt, dass eine Ziffer in der Geheimnummer doppelt vorkommen muss, ergeben sich folgende Möglichkeiten:
Es gibt also zwei verschiedene Möglichkeiten, die Mia ausprobieren müsste.
|
Download | |||||||||||||||||||
| Da schon bekannt ist, dass "ZeigeLinks" = 2 ist, kann man über die Berechnung der Einerstelle ("DaumenRunter" · "ZeigeLinks" = 2) ermitteln, dass "DaumenRunter" = 1 sein muss. Als nächstes schaut man sich die Berechnung der Hunderterstelle an ("ZeigeRechts" · "ZeigeLinks" = 2) Da man schon weiß, dass "ZeigeLinks" = 2 ist, muss also "ZeigeRechts" = 6 sein. Wenn man danach zur Zehnerstelle zurückgeht, weiß man auch, dass "DaumenHoch" = 3 ist, denn sonst würde die dazugehörende Rechnung "DaumenHoch" · "ZeigeLinks" = 6 nicht zu lösen sein. Bleibt noch die Rechnung der Tausenderstelle: "Victory" · "Victory" = 11. Von der Rechnung der Hunderterstelle haben wir noch einen Übertrag übrig. Daher muss "Victory" = 5 sein, damit die Rechnung aufgehen kann.
Die vollständig gelöste Rechnung lautet dann: 5631 · 2 = 11262 |
Download | |||||||||||||||||||
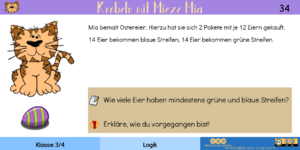
| Bei dieser Aufgabe steht vor allem die Frage im Vordergrund, welche Rechnung in welcher Reihenfolge durchgeführt werden - und was am Ende mit den Einzelergebnissen gemacht werden muss. Tipps an die Schüler könnten also vor allem in diese Richtung gehen.
Da Mia 54 Bonbons geschenkt bekommen hat, 7 Bonbons aber selbst essen möchte, bleiben ihr zum Verteilen nur noch 47 Stück. 8 + 7 · 3 + 4 = 33 Bonbons werden an eine fest vorgegebene Zahl von 16 Freunden verteilt. Es bleiben also 14 Bonbons übrig, die sie an "den Rest" verteilt, jeweils 2 Bonbons pro Kind. Somit werden diese 14 Bonbons also an 7 Kinder verteilt. Insgesamt verteilt Mia ihre Bonbons also an 23 Freunde - und sich selbst. |
Download | |||||||||||||||||||
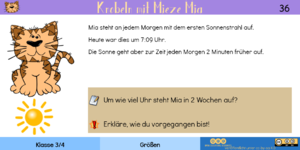
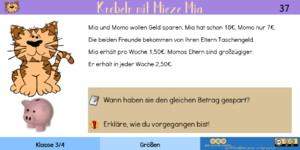
| Für die richtige Lösung dieser Aufgabe ist eine Skizze hilfreich. Daher sind direkt unter der Aufgabe die 4 Wegpunkte des 2,6 km langen Weges dargestellt.
Zuerst lässt sich recht einfach bestimmen, wie weit der Weg von Momo zum Spielplatz ist: Wenn Mia zu Momo geht, legt sie 2,6 km zurück. Geht sie jedoch nur bis zum Spielplatz, dann ist der 2,08 km lang. Also muss der Weg vom Spielplatz zu Momo 2,6 km - 2,08 km = 0,052 km lang sein. Geht nun Momo bis zur Kirche, dann ist sein Weg 700 m lang. Zieht man hiervon nun die Wegstrecke ab, die er erstmal bis zum Spielplatz geht, dann erhält man als Ergebnis die Wegstrecke vom Spielplatz bis zur Kirche. 700 m - 520 m = 180 m. Spielplatz und Kirche liegen also nur 180 m auseinander. |
Download | |||||||||||||||||||
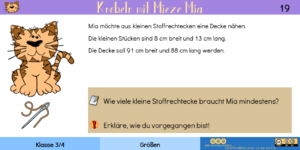
Als Hilfsmittel für die Lösung dieser Aufgabe bietet sich eine Rechentabelle an. Beim Ausfüllen der Tabelle ist jedoch zu beachten, dass der Zuwachs beim Schal nicht in gleichen Schritten erfolgt, sondern Mia jeden Tag ein bisschen mehr schafft, weil sie mehr Übung beim Stricken hat. Dies sprachlich zu erfassen und bei der Rechnung umzusetzen, dürfte für die Kinder die größte Hürde sein. An dieser Stelle könnten also erste Tipps ansetzen (neben dem Hinweis auf die Verwendung einer Rechentabelle).
Da Mias Schal 250 cm lang werden soll, wird sie ihren Schal erst am Freitag fertiggestellt haben. |
Download | |||||||||||||||||||
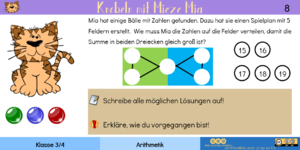
| Die Lösung der Aufgabe wir etwas einfacher, wenn sich im ersten Schritt überlegt, welche Bälle/Zahlen überhaupt nur für das mittlere Feld in Frage kommen. Die Zahlen 16 und 18 scheiden hierbei aus, da die Summe der verbleibenden 4 Bälle dann ungerade wird. Eine ungerade Summe lässt sich jedoch nicht gleichmäßig auf beide Quadrate verteilen.
Somit ergeben sich folgende Möglichkeiten:
Diese drei Lösungen lassen sich natürlich gespiegelt aufschreiben, wodurch es 6 Lösungen gäbe. Zudem gibt es für jede Lösung noch 4 verschiedene Varianten, die 4 Bälle auf die Felder zu verteilen. Dann wären es sogar 24 verschiedene Möglichkeiten. Hier kann jedoch im Gespräch mit den Schülern besprochen werden, ob diese Varianten jeweils als verschiedene oder identische Lösung gewertet werden sollen. |
Download | |||||||||||||||||||
| Um die Länge der Leine zu ermitteln, muss man zuerst die Einzellängen der Wäschestücke mit den jeweiligen Breiten multiplizieren. Die 4 Bettlaken sind 3,8m breit, die T-Shirts 2,1m. Die 10 Socken sind zusammen 1,20m breit. Somit ergibt sich schonmal eine Gesamtbreite von 7,1 m. Insgesamt sind es 20 Wäschstücke, so dass es 19 Zwischenräume á 10cm gibt, was dann in der Summe 1,90m Zwischenraum ergibt. Die Wäscheleine sollte also mindesten 9m lang sein. | Download | |||||||||||||||||||
| Einen echten Lösungsweg gibt zu dieser Aufgabe nicht, da die Aufgabe idealerweise kopfgeometrisch gelöst wird. Bei mentalen Auseinanderbauen des Quaders wird man feststellen, dass sich in der 2. und 3. Schicht in der Mitte je ein Würfel befindet, der keinen Außenkontakt hat. Diese beiden Würfel werden folglich auch nicht angemalt, wenn Mia den großen Quader von außen bemalt. Folglich hat Momo mit seiner Aussage nicht recht. | Download |
</popup>
<popup name="Aufgabe 11-20">
| Aufgabe | Lehrerkommentar | PDF-Vorlage |
|---|---|---|
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt nohc | Download |
</popup>
<popup name="Aufgabe 21-30">
| Aufgabe | Lehrerkommentar | PDF-Vorlage |
|---|---|---|
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download |
</popup>
<popup name="Aufgabe 31-40">
| Aufgabe | Lehrerkommentar | PDF-Vorlage |
|---|---|---|
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download |
</popup>
<popup name="Aufgabe 41-50">
| Aufgabe | Lehrerkommentar | PDF-Vorlage |
|---|---|---|
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt nohc | Download |
</popup>
<popup name="Aufgabe 51-60">
| Aufgabe | Lehrerkommentar | PDF-Vorlage |
|---|---|---|
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download |
</popup>
<popup name="Aufgabe 61-70">
| Aufgabe | Lehrerkommentar | PDF-Vorlage |
|---|---|---|
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt nohc | Download |
</popup>
<popup name="Aufgabe 71-80">
| Aufgabe | Lehrerkommentar | PDF-Vorlage |
|---|---|---|
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt nohc | Download |
</popup>
<popup name="Aufgabe 81-90">
| Aufgabe | Lehrerkommentar | PDF-Vorlage |
|---|---|---|
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt nohc | Download |
</popup>
<popup name="Aufgabe 91-100">
| Aufgabe | Lehrerkommentar | PDF-Vorlage |
|---|---|---|
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt noch | Download | |
| fehlt nohc | Download |
</popup>
| Alle Aufgaben in einer Datei Zur Infoseite mit Lizenzhinweisen
je 3 Kopien pro Seite |
| Alle Aufgaben in einer Datei Zur Infoseite mit Lizenzhinweisen
je 3 verschiedene Aufgaben pro Seite |
Material
| Etiketten Knobelkartei 3/4 Zur Infoseite mit Lizenzhinweisen
je 8 verschiedene Etiketten pro Seite |
| Etiketten Knobelkartei 3/4 Zur Infoseite mit Lizenzhinweisen
je 8 gleiche Etiketten pro Seite |
| Arbeitsheft Knobelkartei Zur Infoseite mit Lizenzhinweisen
Arbeitsheft zum Einkleben der Kartei-Etiketten |